摘要
一定合理的井壁坍塌对于缓和井壁稳定与储层保护之间的矛盾具有重要作用。本文通过分析影响井壁坍塌的主控因素,采用BP神经网络算法实现对井壁坍塌程度的预测。相较于依靠传统经验公式预测井壁坍塌程度,该种方法的预测结果更为科学可靠。结果表明:通过BP神经网络模型对井壁坍塌程度的预测结果与现场实测值绝对误差率为0.37%~14.22%,平均误差率为7.54%。预测精度满足工程精度,证明了BP神经网络预测井壁坍塌程度的可行性。
Abstract
Some reasonable wall collapse to ease the contradiction between wall stability and reservoir protection plays an important role. Through the analysis of the main factors affecting the wall collapse. Using the BP neural network algorithm to predict the degree of wall collapse, than the traditional experience formula to predict the degree of wall collapse, the prediction result of this method is more scientific and reliable. The results show that the absolute error rate of the prediction result of BP neural network model is 0.37%-14.22%, and the average error rate is 7.54%. The prediction accuracy satisfies the engineering accuracy, proving the feasibility of the BP neural network to predict the degree of well wall collapse.
Keywords
0 引言
随着中国经济社会的高速发展,对石油天然气等能源资源的需求日渐增加,即便是步入后工业化发展阶段(2030—2035),能源与矿产资源仍然需要保持较高的人均消费水平,中国仍将需要大量的能源与矿产资源作为基础支撑(董延涛等,2023)。由于海上作业成本高、工程难度大等问题,使得海上油田一直未得到有效开采(马世忠等,2021),而井壁稳定是其中的关键课题之一(陈勉等,2008;贾利春等,2017;朱忠喜等,2017;刘向君等,2018)。
渤海湾盆地是中国东部典型的富油型湖湘盆地(许鹏等,2022),拥有丰富的油气资源,现阶段的主力开发层为东营组和沙河街组,属于中深部地层,相比于浅部地层,渤海湾油田深部地层具有岩性条件复杂、油藏环境复杂、井壁稳定性差等一系列突出问题,对钻井作业的安全运行造成了极大困难,也极大的增加了钻井的经济成本。其中,以绥中某油田该类问题尤为突出,其东营组段的泥岩局部含灰质的情况较为严重,表现为中硬地层,岩屑呈块状,表现为较强的各向异性,极易造成岩屑上返困难,甚至发生卡钻等一系列钻井事故,加剧井壁坍塌的风险。对于沙河街组,由于该段含有大量火成岩,大大增加了裂缝性漏失的危险。
对井壁坍塌的预测,掌握井壁坍塌规律,是采取有效的预防和应急预案,最大程度减少和杜绝钻井事故,提高钻井作业质量和采收率的有效途径。因此,针对绥中某油田中深部地层地质情况复杂,基于现场测井数据,通过主成分分析法筛选出影响井壁稳定的主要影响因素,借助神经网络优化算法,预测井壁坍塌,为进一步合理规划钻井液密度、制定井壁失稳应急方案和降低绥中某油田作业风险提供参考。
1 BP神经网络建模
1.1 基本原理
BP神经网络是由输入层、隐藏层和输出这3个部分所构成的多级前馈神经网络(王一妹等, 2021)。一个3层的BP神经网络模型可以高度拟合任何函数(曾宪奎等,2019),可以对钻井参数和井壁坍塌程度之间的非线性关系进行学习,当误差达到最小时进行坍塌程度预测。其中,BP神经网络中的学习速率是决定迭代过程中的更新步长的关键 (陆冬,2017;王文鹏,2022)。不恰当的学习速率会严重影响BP神经网络预测的训练效率与精度,具体表现为学习速率过大,容易造成震荡,学习速率过小导致收敛速度过慢。
通过BP神经网络进行坍塌预测,不但能够准确地捕捉到各种因素之间的复杂关系,准确地预测井壁坍塌程度,还能实现历史数据自主学习,从中发现隐藏的模式和规律。这种数据驱动的方法更客观、准确地反映实际情况,避免了人为因素对预测结果的影响。
1.2 影响井壁坍塌因素的优选
利用钻井参数对井壁坍塌程度进行预测,要以不同井壁坍塌程度具有不同的钻井参数响应特征为基本原则和依据。在钻进过程中,由于不同层位的岩石可能具有不同的力学性质,这就会导致某些钻井参数不具有特征性或特征性不明显,不能反应实际情况,导致参数之间的相关性较弱,这对于井壁坍塌程度最终预测值的精度造成直接影响。
1.2.1 参数的优选原则
(1)参数范围设定:进行参数优化时,需要筛选参数取值范围,剔除异常数据。合理的参数范围可以避免优化过程无法收敛或陷入局部最优解的问题。
(2)优化算法选择:选择合适的优化算法是参数优化的关键。不同的优化算法适用于不同类型的问题。常见的优化算法包括梯度下降法、遗传算法、粒子群优化等。其中,梯度下降法适用于寻找最小化目标函数(损失函数)的参数值,而预测井壁坍塌的问题可以转化为一个回归问题,即最小化预测值与实际值之间的误差,且梯度下降法在训练神经网络时具有较高的计算效率和稳定性,可以快速地迭代更新网络参数,从而在较短的时间内得到较为准确的预测结果,因此,本文选择梯度下降法对神经网络的预测进行优化。
(3)终止条件设定:进行参数优化时,需要设定恰当的终止条件。设置合适的终止条件可以避免不必要的计算开销和优化过程的过度。常见的终止条件包括达到训练误差达到预设阈值、迭代次数达到预设上限、交叉验证等(表1)。
表1终止条件分析

1.2.2 钻井参数的优选方法
因子分析法是一种从研究指标与相关矩阵自身之间的相互依赖关联关系入手,将若干信息相互交叉的变量,归咎于少数几个互不有关的组合变量的一类多元统计分析方法。它的关键核心是寻求潜藏在多个不同变量数据中、不能被直接注意到却可以对最终结果有一定影响的潜在因子,并进一步预测该类因子对最终结果的影响程度以及各潜在因子之间的内在联系与关联程度。因子分析法分析变量的关键点是筛选出核心因子,用最少的相互独立的因子去描述需要多变量才能表述的信息(刘振明等,2018)。
1.3 神经网络的预测训练
(1)参数初始化
将引起井壁坍塌的主要因素作为输入层,用m 来表示,而井壁坍塌情况作为唯一一个输出数据,即输出层,用n来表示,用k来描述隐含层,进一步得到初始权值和阈值。并建立基本的BP神经网络算法的基本框架(李海锋,2018;乔俊飞等,2018;Hos sein et al.,2021),标定目标误差、迭代次数以及其他参数。
(2)隐含层输出
根据输入的数据序列,即井壁坍塌主成分数据向量X={X1,X2,···,Xn },可由(式1)计算得出,并输出隐含层。与连接权值Sij 计算BP神经网络的隐含层输出。
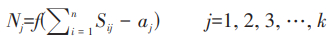
(1)
式(1)中:Nj-隐含层输出;Sij-输入层与隐含层之间的权值;aj-隐含层阈值;f-隐含层激励函数。
常见的激励函数如表2所示,其中Sigmoid函数的应用最为广泛。常用的激励函数(乔俊飞等,2018)
表2常用的激励函数

(3)输出层计算
根据第2步所输出的Nj,以及隐含层至输出层连接权值Sj 和输出层的阀值,对BP神经网络的预测值进行输出,可由式(2)计算得出:
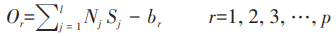
(2)
式(2)中:Or-预测的输出结果;Sj-输入层与隐含层之间的权值;br-输出层阈值。
(4)误差计算
根据第3步的预测输出Or 与输入的期望输出 Yr,计算神经网络的误差er,并逆向逐层传递,进一步求出各层的误差:
(3)
式(3)中:er-预测误差;Yr-期望输出;Or-预测的输出结果。
(5)权值更新
分析误差计算中的逆向偏导函数的斜率,采用随机梯度下降和附加动量项的方法对所有权值和阈值进行优化(杨博远,2021),以运算误差为判断基准进行循环训练,若运算误差满足目标期望值,训练结束,否则进行第2步,根据输出期望和训练样本重新开始开始训练,可由式(4)、式(5)计算得出:
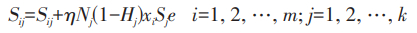
(4)
(5)
式(4)、(5)中:η-学习率;xi-第i个影响井壁坍塌因素的数据;Sj-输入层与隐含层之间的权值;
(6)阀值更新
根据上一步骤中的预测误差ek,更新神经网络阀值m和n,计算公式如下所示:
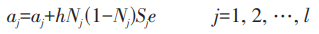
(6)
(7)
式(6)、(7)中:br-输出层阈值。
(7)根据上述步骤进行迭代计算,如果到达算法所需的迭代精度,则停止迭代,否则返回隐含层重新计算。BP神经网络井壁坍塌预测流程如图1所示。
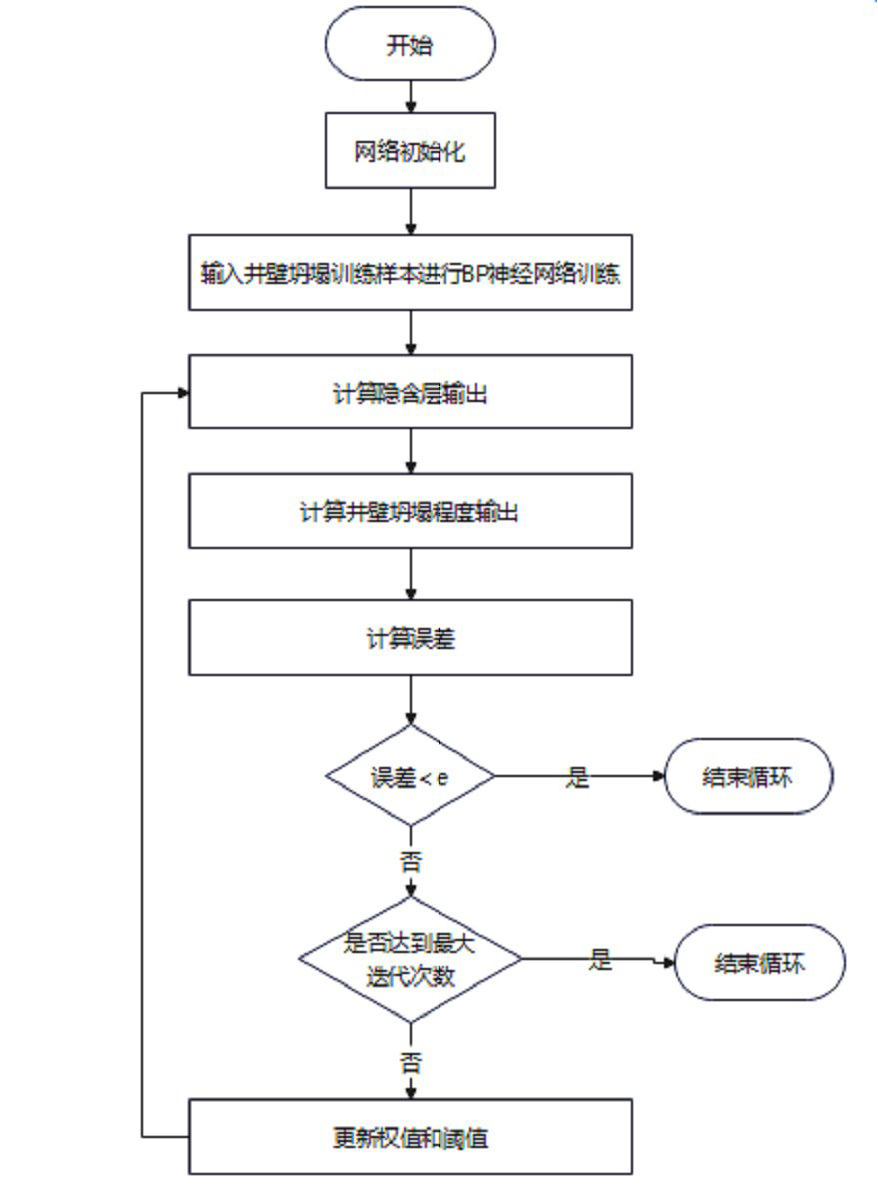
图1BP神经网络井壁坍塌预测流程图
2 实例应用
2.1 目标区域概况
目标井SZ-A位于绥中某油田,其构造位置位于渤海辽东湾海域,完钻井深为3200 m,从浅部地层至深部地层分别为明化镇组、馆陶组、东营组、沙河街组和中生界,目的层位为沙河街组。
2.2 样本数据获取与优选
2.2.1 基本参数的选择
钻井基本参数的选择对预测井壁坍塌至关重要,因此所选择的参数必须能够全面、准确地反映井壁坍塌的关键因素,并基于这些参数建立有效的预测模型。参数的选择主要考虑以下方面:
(1)地质环境的复杂性
井壁周围的土体和岩石性质对井壁的稳定性起着决定性作用。摩擦角、黏聚力、孔隙压力等参数直接反映了土体的物理性质和强度,对于预测井壁的稳定性至关重要。
(2)应力的影响
井壁所受的应力状态(最大水平主应力、最小水平主应力)是影响井壁稳定性的重要因素。在钻井过程中,由于应力状态的改变,可能会导致井壁坍塌。
(3)上覆岩层压力
上覆岩层压力体现了上方岩层对井壁的压力,与井壁的稳定性密切相关
(4)黏土的物理性质
泊松比作为一个描述材料物理性质的参数,能够反映材料在受到外部压力时的变形特性,对于井壁的稳定性有一定的影响
因此,使用这7个参数进行井壁坍塌的预测,能较为准确地评估井壁的状态,并提供有效的预防措施和建议,确保钻井过程的安全进行。且通过实时监测这些参数的变化,可以及时发现井壁可能存在的问题,为预防坍塌提供预警。
2.2.2 样本数据的优选
在绥中某油田井壁坍塌程度预测的研究中,对 SZ-A井的钻井参数间的相关性采用因子分析法进行优化,从而达到减少干扰信息、提高BP神经网络预测模型可靠度的目的。
首先对内摩擦角(φ)、黏聚力(C)、孔隙压力 (PP)、最大水平主应力(σH )、最小水平主应力(σh)、泊松比(μ)、上覆岩层压力压力(σv )7个相关参数进行方差分析,分析结果见表3。从主因子方差分析可得出,此次共有7个主成分被提取出来,取方差贡献率前2的主成分,分别命名为第一主成分和第二主成分,由于其该两种主成分累计贡献率达到了 88.578%,保留了原始钻井参数的绝大多数信息。因此研究层位的各钻井参数可用前2个主成分来进行表示。
通过最大方差法来对表2中所得的前2个主成分进行旋转分析,并进一步建立旋转成分矩阵,如表4所示。其中,孔隙压力、最大水平主应力和最小水平主应力这3种力与第一主成分的相关性均大于 85%;内摩擦角、泊松比、黏聚力和上覆岩层压力这 4类参数与第二主成分相关性均大于70%。
表3主因子方差分析

表4旋转成分矩阵
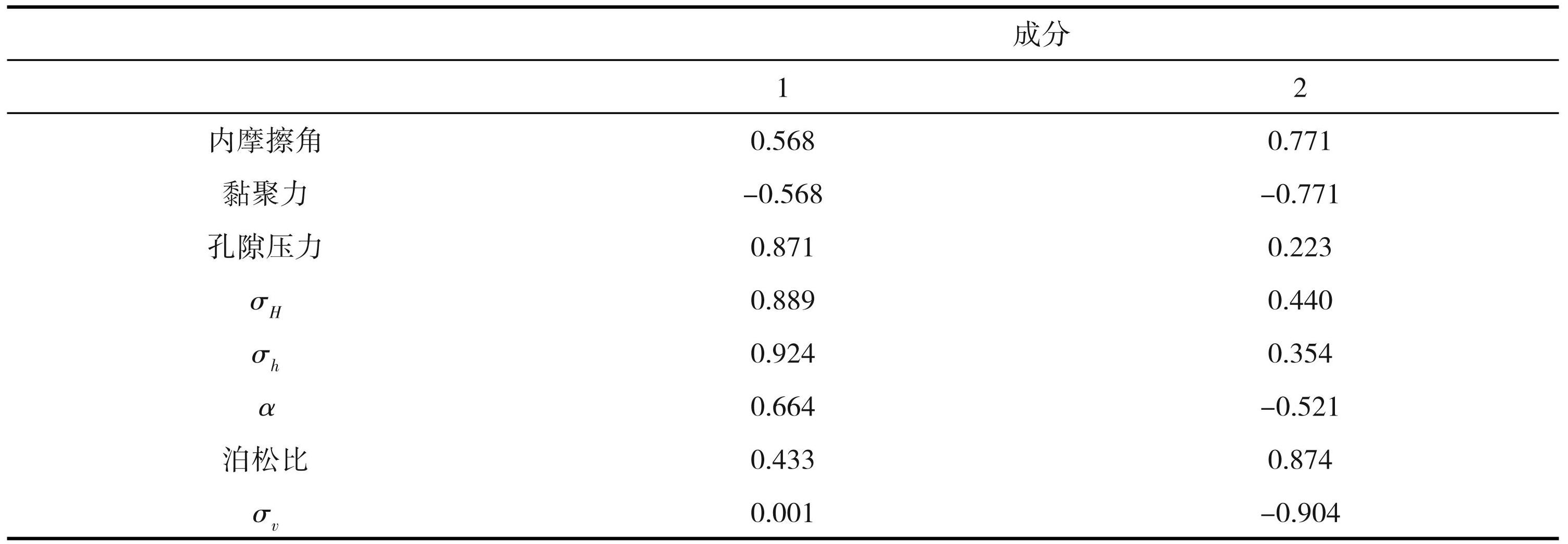
结合以上分析结果,绥中某油田SZ-A的井壁坍塌程度主要与内摩擦角、黏聚力、孔隙压力、最大水平主应力、最小水平主应力、泊松比和上覆岩层压力的关联度较为明显,因此可以将这七个参数作为BP神经网络的输入参数(图2)。
2.2.3 基础数据选取
通过井壁坍塌原因进行多方面分析,确定了影响井壁坍塌的7个因素,内摩擦力、黏聚力、孔隙压力、最大水平主应力、最小水平主应力、泊松比和上覆岩层压力,由于神经网络训练的样本数量至少是自变量的10倍(Kim et al.,2019),因此,本文根据7 个参数,共选取了1800组数据。如表5所示。
2.3 BP神经网络预测参数设置
(1)参数设置原则
各项参数的初始值设置都是根据经验或者相关文献和实际应用中的推荐值来进行设定,对于常规的预测,学习率的设定值一般为0.01~0.1,最大迭代次数一般为1000~10000,最小误差的设定值一般为0.00001~0.001。具体赋值须遵循以下原则:
①问题的性质和复杂性,对于不同性质和复杂性的问题,需要设定不同的参数值。对于简单问题,可以设置较大的学习率和较小的训练误差,以便更快地收敛;而对于复杂问题,则需要设置较小的学习率和较大的训练误差,以便更精确地逼近最优解。
②数据规模和分布,数据规模和分布也会影响参数的设定。数据规模较大,需要更多的迭代次数来充分训练网络;数据分布较为复杂,需要更小的学习率和更精确的训练误差。
③经验和实践,参数的设定也与经验和实际应用有关。根据实践经验,可以设定一个合理的初始值,然后在训练过程中调整参数,以获得最佳的训练效果。
(2)参数优化方法
在训练过程中,可以根据性能评估的结果动态调整学习率或迭代次数。当训练陷入局部最优时,可以尝试减小学习率、增加迭代次数以跳出局部最优;反之,当训练发散时,可以增大学习率或减少迭代次数以加速收敛。
表5BP神经网络模型样本数据

(3)预测参数设置
本文选取3层BP神经网络近似估算井壁的坍塌程度。BP神经网络的参数设置:输入参数为7 个,输出参数为1个,隐含层节点个数M根据经验公式(朱正东等,2022;Sun et al.,2023)M=2n+1(n为输入节点个数)确定为16;把最大迭代次数设置1000,学习率设定为0.02,训练最小误差为设置在0.001。隐含层的激活函数选用Sigmoid函数,输出层的激活函数设定为Purelin函数(白超等,2018;尤游和张林静,2022)。
2.4 预测结果验证
在SPSS平台上进行结果分析,预测1500组数据的井壁坍塌程度。为了验证预测的普遍性,首先从表5的1500组数据中随机选取1125组数据作为 BP神经网络的训练集,剩余375组数据作为测试集。将影响井壁坍塌的7个参数作为输入量,扩径率作为输出量,建立参数与扩径率之间的非线性映射关系。预测结果如表6所示。

图2BP神经网络结构示意图
表6BP神经网络模型预测结果

为验证所构建的井壁坍塌程度预测的神经网络模型的可实用性,在表4所列出的1500组数据中随机抽取100组数据进行线性拟合,得到多元回归方程:
(8)
式(8)中:井壁扩径率(%);φ-内摩擦角(°);黏聚力(MPa);PP-孔隙压力当量密度(g/cm3);σH-最大水平主应力当量密度(g/cm3);σh-最小水平主应力当量密度(g/cm3);μ-泊松比,无量纲;σv-上覆岩层压力当量密度,g/cm3。
用式(8)对剩余的1400组数据随机抽选的25 组进行检验,其拟合结果如图3所示。对比可知,基于因子分析的BP神经网络预测模型具有更高的精度。多种钻进参数获得的数据是多元的,全部使用势必会引入噪声数据。在神经网络建模的过程中,利用因子分析法可完成输入参数的选择,达到进一步优化模型的目的(图3)。
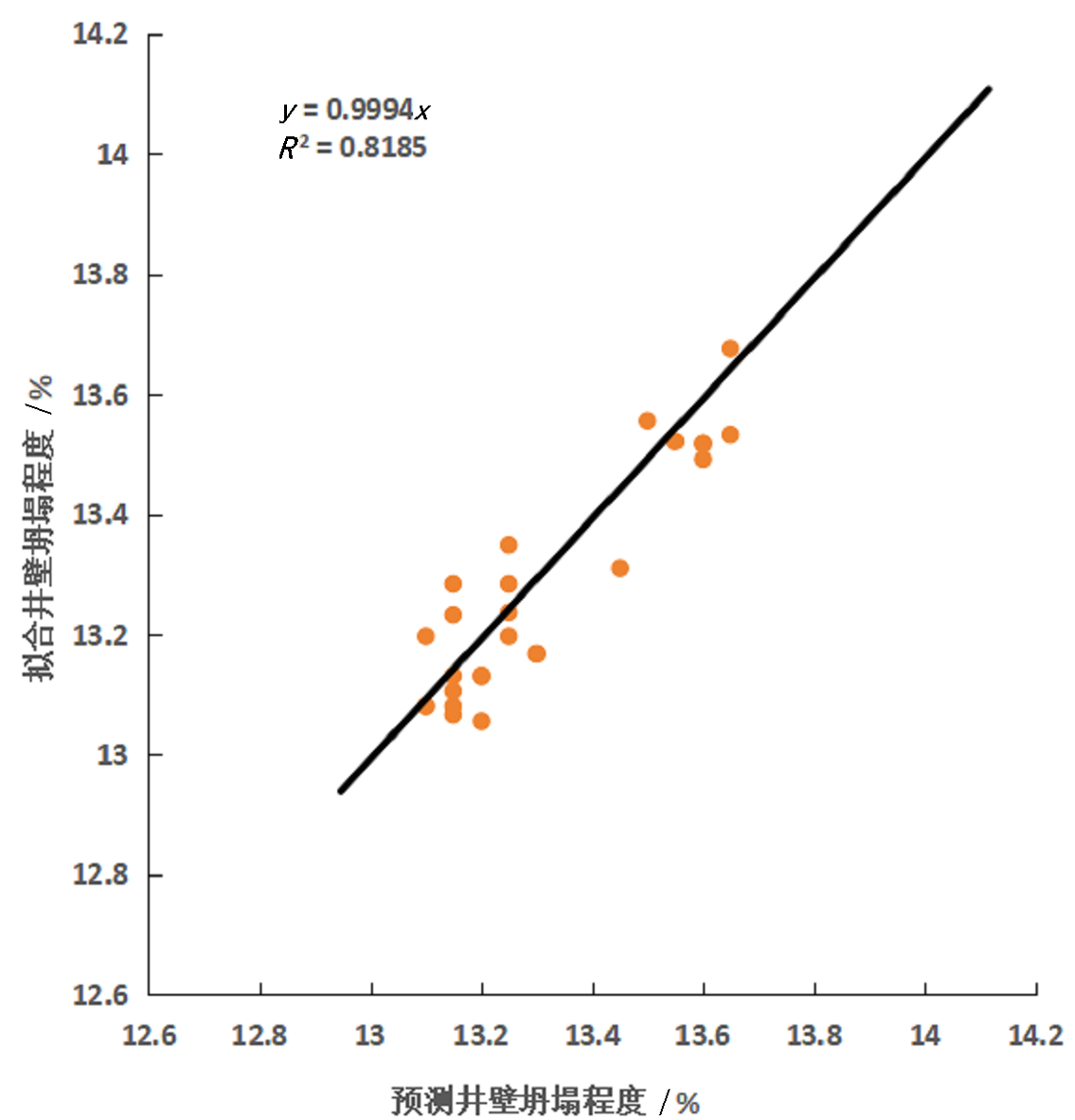
图3多元回归分析曲线拟合结果
2.5 预测结果分析
2.5.1 模型误差分析
1)误差率的计算
BP神经网络预测井壁坍塌的误差率的计算方法通常是通过比较预测结果与实际结果之间的差异来确定的。具体来说,可以将预测结果与实际结果进行对比,计算出每个数据点的误差,然后根据这些误差计算出整体的误差率。误差率的计算方式如下:
(9)
式(9)中:λ-误差率(%);η1-井壁实际坍塌率 (%);η2-预测井壁坍塌率(%)。
2)误差产生的原因及影响
(1)误差产生原因
误差主要来源于数据采集、特征提取、模型训练和预测等多个环节。
①数据采集。受到传感器精度、环境因素等影响,导致数据存在噪声或偏差。
②特征提取。可能由于特征选择不当或特征提取方法不准确,导致提取的特征不能完全反映井壁坍塌的内在规律。
③模型训练。可能由于学习率、迭代次数等参数设置不合理,导致模型无法收敛到最优解或陷入局部最优解。
④预测过程。可能由于模型参数或结构的随机性,导致预测结果存在偏差。
(2)对结果准确性的影响
误差对预测结果准确性的影响取决于误差的大小和性质。如果误差较小,对预测结果的影响也会较小;如果误差较大,可能会导致预测结果偏离实际情况,从而影响预测的准确性和可靠性。因此,在应用BP神经网络进行井壁坍塌预测时,需要综合考虑数据质量、模型结构、训练方法、参数设置等多个因素,以提高预测结果的准确性。同时,也需要不断优化和改进模型,以降低误差率,提高预测的准确性和可靠性。
3)误差的减小
为了减小误差对预测结果准确性的影响,可以从如下途径进行考虑:
(1)优化数据采集和预处理过程,提高数据的质量和准确性;
(2)改进特征提取方法,选择更有效的特征和特征组合,提高特征的表示能力;
(3)调整模型训练的参数和优化算法,提高模型的收敛速度和精度;
(4)对模型进行交叉验证,选择最佳的模型参数和结构,提高模型的泛化能力。
2.5.2 预测结果分析
通过构建BP神经网络模型,预测绥中某油田 SZ-A井井壁坍塌程度。预测结果表明:BP神经网络模型对井壁坍塌程度预测结果与现场实测值绝对误差率为0.37%~14.22%,平均误差率为7.54% (图4)。且基于BP神经网络的预测模型可以有效避免经验公式估算引起的误差,预测精度满足工程精度,证明了BP神经网络预测井壁坍塌程度的可行性(图5、图6)。

图4井壁扩径实测值与预测值密度分布图
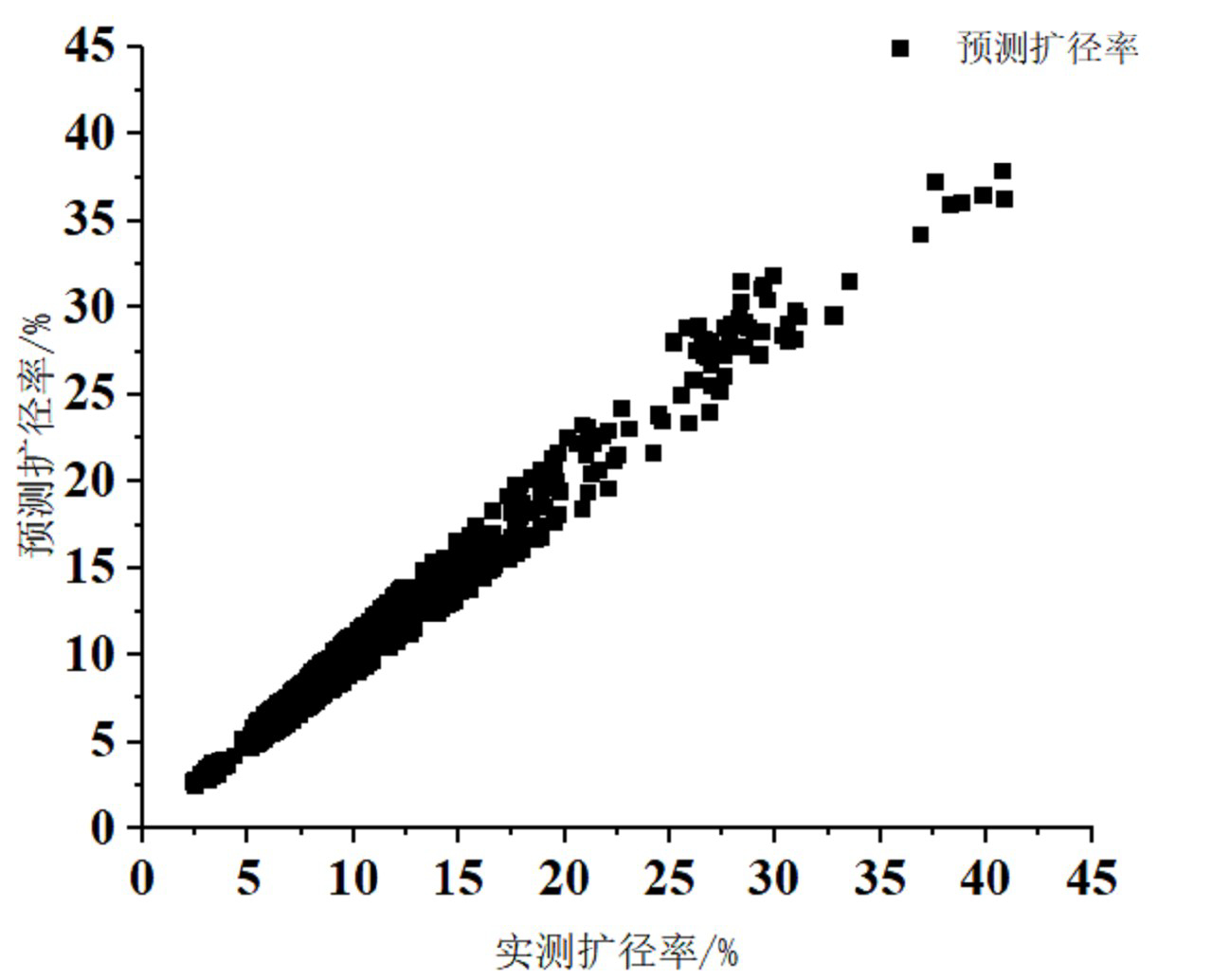
图5井壁扩径实测值与预测值分布图
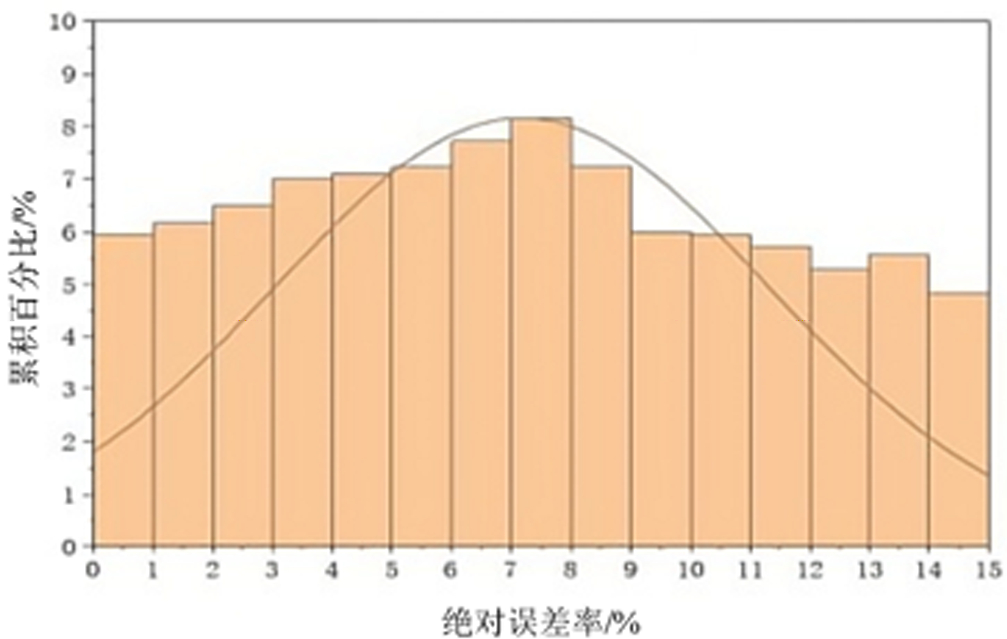
图6预测结果精度分布统计图
2.6 模型适应性评估
BP神经网络模型在岩石力学问题中,特别是在不同的地质条件和钻井环境下,具有一定的适用性和限制。
(1)适用性:
①岩石分类与识别:通过BP神经网络,使其能够学习并识别不同类型岩石的特征,包括其物理性质、化学成分等,为钻井设计提供依据。
②岩石破裂预测:通过分析岩石的应力、应变等数据,神经网络可以学习并识别出岩石破裂的模式和规律。可以更好地设计钻井的参数,避免因岩石破裂而导致的钻井事故。
③岩石力学参数反演:通过分析岩石的应力、应变等实测数据,神经网络可以学习并估算出岩石的力学参数,如弹性模量、泊松比等,优化钻井设计和施工方案。
(2)限制性:
①数据获取与处理:对于BP神经网络而言,需要大量的数据作为训练样本。然而,在岩石力学问题中,数据的获取和处理存在一定的难度。岩石的应力、应变等数据需要高精度的测量设备,且数据处理的算法也需要根据具体情况进行定制和优化。
②模型泛化能力:虽然BP神经网络具有较强的泛化能力,但当遇到新的地质条件或钻井环境时,神经网络的预测精度可能会受到影响。此时,需要对神经网络进行重新训练或调整,以适应新的情况。
③模型解释性:BP神经网络是一个黑箱模型,其决策过程缺乏透明度。对于一些需要解释性结果的场景,如钻井设计决策、岩石分类等,使用BP神经网络可能存在一定的限制。
3 结论
(1)基于BP神经网络的预测模型可以有效避免经验公式估算引起的误差,预测精度满足工程精度要求,证明了BP神经网络预测井壁坍塌程度的可行性。
(2)钻井参数在数值上的不同特征响应了井壁坍塌的不同程度。通过引入井壁坍塌度的概念,建立了井壁坍塌程度与钻井参数之间的联系。
(3)BP神经网络预测模型具有应用范围广、非线性映射能力强和精度高的特点。相对于常规多元回归模型,该模型能更明确地表示井壁坍塌程度和各个参数间的关联性。
(4)此外,如何进一步神经网络算法中一些预测精度,使得所预测结果更符合现场实际,也是需要解决的问题。
致谢 在论文撰写过程中,得到吴慧梅老师的大力支持,对我论文的修改提出了许多宝贵意见,也从课题组其他成员获取了许多帮助,在此一并感谢。











