摘要
平谷区处于京津冀的几何中心位置,地质灾害频发,严重影响着区域社会稳定与发展建设,开展地质灾害风险评价正是支撑区域地质灾害防治与风险管理的重要一环。为有效避免地质灾害风险评价主观因素影响和评价因子量纲不统一的问题,本文以北京市平谷区为研究区,基于GIS平台应用,利用DEA方法中的SE-SBM-DEA和DEA-CCR模型分别开展危险性和易损性评价,并通过Tobit回归模型来避免因子的相关性干扰,综合叠加完成平谷区地质灾害风险评价。评价结果显示:极高风险区、高危险性区域占全区面积的27.63%,占总灾害点数量的86.3%,灾害点分布与风险区划分具有很好的相关性,证明了DEA方法在地质灾害风险评价中的适用性,也可为平谷区地质灾害防治工作提供参考依据。
关键词
Abstract
Pinggu District is at the geometric center of Beijing-Tianjin-Hebei region. The frequent occurrence of geologic disasters in the region seriously affects the social stability and development of the region. Therefore, geohazard risk evaluation is an important part to support regional geohazard prevention and risk management. This study takes Pinggu District of Beijing as the study area. Based on the GIS platform application, the SE-SBM-DEA and DEA-CCR models in the Data Envelopment Analysis (DEA) framework were utilized to carry out hazard and vulnerability evaluations, respectively. And the Tobit regression model is employed to avoid the correlation interference of factors, and the comprehensive superposition completes the regional geohazard risk evaluation. This method can effectively avoid the influence of subjective factors in geohazard risk evaluation and the problem of inconsistency of evaluation factors. The results show that the extremely high-risk area and high-risk area account for 27.63% of the total area of the district and 86.3% of the total number of disaster points. There is a good correlation between the distribution of disaster points and the division of risk zones. The applicability of the DEA method in geologic disaster risk evaluation is proved. The results provide a reference basis for the prevention and control of geologic disasters in Pinggu District.
0 引言
地质灾害风险评价是综合考虑了自然和社会属性,对风险地区地质灾害的概率和后果进行定量分析和评估,并采取适当措施降低灾害发生的可能性(齐信等,2012)。地质灾害的产生是复杂且非确定性的一种现象,根据评价类型、评价内容的不同,现有的地质灾害评价模型也较为多样,通常包括危险性评价和易损性评价两部分评价内容。“危险性” 是自然属性特征的体现,主要考虑的是发生评价地质灾害历史活动和未来地质灾害发生概率;易损性是承受特定灾害时候的综合能力的量度,是承灾体抵御能力的社会属性特征的体现(程凌鹏等, 2001)。1992 年联合国人道主义事务部提出“风险度(risk)=危险度(hazard)×易损度(vulnerability)”的表达式,如今国内外专家和学者普遍认为“风险是对存在两个或者两者以上结果的不确定性的一种度量”,在地质灾害风险评价中一般认为风险性=危险性×易损性(齐信等,2012)。常见的地质灾害风险评价(包括危险性或易损性)评价方法可以分为以下4类:主观赋权法(层次分析法、网络分析法、德尔菲法等)、基于统计分析模型(信息量模型、模糊综合评价法、证据权模型、线性回归、粗糙集、人工神经网络模型、数据包络分析、逻辑回归等)、确定性模型方法(地质工程方法)及机器学习方法(KNN 最近邻算法、集成算法、人工神经网络等),而数据包络分析法(DEA)正是一种基于统计分析的不确定性模型。
Charnes et al.(1978)提出了第一个 DEA 模型 C²R 模型,后期经学者们不断研究又拓展出多种模型,包括 BBC 模型、FDH 模型、加性 DEA 模型、Rus‐ sell测度模型、交叉效率DEA模型、超效率DEA模型以及基于松弛变量测度SBM-DEA模型和网络DEA 模型等(李红和朱建平,2012;赵天毅,2021)。DEA 方法特别适用于具有多输入多输出的复杂系统,能够同时考虑多个不同类型的投入和产出变量,适用于复杂的生产或服务系统效率评估,在医院运营效率、企业生产效率、教育资源配置、城市资源利用等方面得到了广泛应用。
在地质灾害风险评价过程中自然属性和社会经济属性指标均属于客观数据,相较于其他方法而言DEA方法通过线性规划的方法基于相对效率,不需要事先设定函数形式与量纲处理,从最有利于评价决策单元的角度产生权数,避免了因错误设定函数形式而导致的评估偏差和主观因素影响及量纲处理后产生的不利影响。邹毅等(2011)利用 DEA-CCR模型进行崩塌地质灾害风险研究,便捷地得到了较为理想的评价结果,减少了主观因素的干扰。吕军等(2013)运用两次超效率DEA模型,定量地分析出了中国各省(市)的地质灾害易损性情况和地质灾害防治效率水平,所得结果大体上与客观现实情况相符;王小丽(2013)结合 RS 与 GIS 技术,运用 DEA-CCR 模型对伊犁谷地地质灾害易损性进行评价。顾春杰等(2014)将 DEA 模型和生产函数思想应用到泥石流易损性的评价中。Li et al.(2015)、侯俊东和金欢(2017)、孙浩和杨桂元(2017)分别基于三阶段 DEA 方法、DEA-多元回归模型和交叉 DEA—Tobit模型对相关影响因素进行分析,得出了中国各省市省份的地质灾害的脆弱性且进行了排序,并对各因子敏感度进行分析。Gan et al.(2022) 研究开发了一个两阶段并行系列网络DEA模型,结合了径向和非径向测量来解释输入和输出的非比例变化,确定地质灾害是否对农村发展产生影响。殷启睿等(2021)按所代表的成灾条件将原本的指标重新分类,根据每个成灾环节对应的发灾场、致灾力与灾害体现构建了暴雨泥石流二阶段 DEA 模型,根据因子冗余情况分析成灾特征。由此可见, DEA方法在多类型、多维度的地质灾害评价中均有所应用,与多种方法相结合应用于危险性、易损性分析中,均取得了较好的应用效果。
DEA 方法在国内地质灾害评价中应用起步较晚,在地质灾害领域的应用也较少,利用 DEA 方法开展区域内地质灾害风险评价仍有待于加强研究。现阶段应用多单独应用于区域危险性评价或者省级尺度上的易损性评价,针对区县范围内的应用 DEA方法的地质灾害风险评价相对较少,其指标体系的建立也缺少参考。
本文以平谷区地质灾害风险评价项目为依托,利用 GIS 平台和 R 语言进行统计分析,建立了基于 DEA方法的指标评价体系,利用 DEA方法中的 SE-SBM-DEA 模型和 DEA-CCR 模型分别开展危险性和易损性评价,同时利用Tobit回归分析对选取的相关指标进行显著性检验,利用风险矩阵判别法进行风险评价进而推导出风险评价结果,以期为平谷区的地质灾害提供防治思路与决策参考,同时为其他区域DEA方法应用提供借鉴。
1 研究区概况
平谷区位于北京东北部,东南与天津市蓟州区、东北与河北省承德市兴隆县毗连,地理坐标为东经 116°55″~117°24″,北纬 40°02″~40°22″,东西长 35.5 km,南北宽 30.5 km,面积约 948.24 km2。研究区属北温带大陆性气候,年平均气温为 11.5 °C,年降雨量 621.7 mm,降雨量集中在 7 月下旬和 8 月初,平均降雨量为 375.7 mm,占全年降雨量的 62.2%。该地区河流较多,均属蓟运河水系,其中主要的常年河流有洳河、泃河和金鸡河。研究区位于燕山山脉和华北平原的交汇处,地形由东北向西南倾斜,中心平坦,东南和北部三面环山,山前为环形平山丘陵,中部和南部为冲积型和洪积型平原(图1)。通过资料收集与野外实地调查共确认地质灾害隐患点 694 处(图2),其中崩塌 611 处,占比 88.04%;滑坡 26 处,占比 3.75%;泥石流 48 处,占比 6.92%,地面塌陷 9 处,占比 1.29%。研究区地质灾害多集中于山区,威胁居民点、道路、景区、矿山及水库、其他(农田、森林等)等,集中发育在镇罗营镇、金海湖镇、熊儿寨乡、大华山镇、黄松峪乡等。

图1平谷区地理位置图(a)和地形地貌图(b)
2 基于DEA的风险评价模型
DEA方法是以相对效率概念为基础,用于评价具有相同类型的多投入、多产出的决策单元(DMU) 是否技术有效和规模有效的一种方法(马占新和赵春英,2016)。在区域地质灾害风险评价中,具有足够数量的评价单元和相同投入产出类型,DEA方法可以有效适用。其基本思路是把每一个被评价单元(栅格)作为一个决策单元(DMU),每一个 DMU 都具备同类型“投入”(自然属性或社会属性指标) 和“产出”(地质灾害隐患或威胁对象指标),通过对投入和产出比率的综合分析,以DMU的各个投入和产出指标自行确定的最优权重进行评价运算,确定 “有效生产前沿面”,并根据各DMU与有效生产前沿面的距离状况,确定各 DMU 效率值,效率值越大其风险越高。
本文采用SE-SBM-DEA模型进行危险性评价,同时利用 Tobit 模型对得出的评价结果进行回归分析,可以避免变量之间的多重共线性,有效地验证选取的相关指标的有效性。在易损性评价中,从物质、社会、经济、环境4个方面进行易损性评价,以乡镇为评价单元,其评价单元相对较少仅为 14 个,故采用 DEA-CCR模型便能很好地给出相应的评价结果。

图2平谷区地质构造及灾害隐患点简图
2.1 DEA-CCR模型
DEA 模型,它可以根据一组多输入、多输出值估测出有效生产的前沿面,并且根据这个有效前沿面来对每一个决策单元的生产效率值进行综合效率评判。该模型的优点是不需要主观地对各种指标赋予相对权重,因此更具有客观性。
DEA 的基础模型为基于规模收益不变的投入角度的CCR模型,该模型可如下式表示:
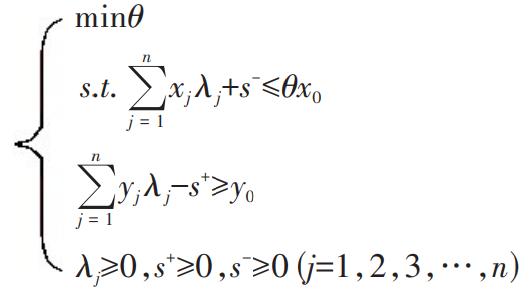
(1)
式(1)中,θ 为各决策单元综合效率,λj(j=1,2,···,n)为权重变量,s- 为投入松弛变量,s + 为产出松弛变量,x0、y0为 DMU0的投入、产出向量;xj、yj为第 j 个 DMU 的输入、输出指标。其中,θ∈(0,1],当 θ=1 时,即此DMU的投入产出水平位于最优生产前沿面上,达到最佳效率;相反,不位于最优生产前沿面上,没有达到最佳效率水平。
2.2 SE-SBM-DEA模型(Super_SBM_VRS)
在 DEA 模型中可分为径向 DEA 模型和非径向 DEA 模型、角度 DEA 模型和非角度 DEA 模型。当出现投入过度或者产出不足的情况,即存在投入或产出的非零松弛(Slack)时,径向 DEA 模型把 DMU 的效率值评估到很高;然而,角度 DEA 需要忽略投入或产出的变动情况,得出了不符合客观实际情况的结果(马占新和赵春英,2016)。因此,为了克服上述问题,Kaoru(2001)创造了一种基于松弛变量的效率测度方法(Slacks-Based Measure)即 SBM模型,但同时SBM模型存在相应的缺陷,其得出的效率值只能维持在(0,1]区间内,有效率的 DMU 其值为 1,而小于 1 的不再进行比较认为是无效的,无法比较有效率的DMU。为了避免这一弊端,Tone构建了超效率 SBM 模型。与径向 DEA 和方向 DEA 的超效率模型相比,SBM 模型要复杂一点,而且只能计算有效率的 DMU。因此,要想使用 SBM 模型得出所有 DMU的可比值,通常都是两种模型的综合结果。
对于 DMU(x0,y0),其规模报酬可变(VRS)的超效率SBM模型表示为:
假设有 n 个决策单元,其投入和产出向量:X=(xij)∈Rm×n,Y=(ykj)∈Rs×n,令 X>0,Y>0 则生产可能性集,如下式:
(2)
式(2)中Λ=[λ1,λ2,λ3,···]∈Rn,表示权系数向量, P函数中的两个不等式分别表示实际投入水平大于前沿水平,实际产出小于前沿产出水平。SE-SBM-DEA模型如下:
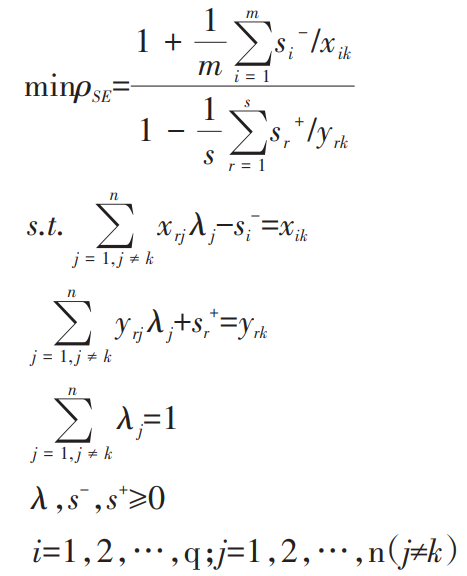
(3)
式(3)中,si ∈Rm,sr∈Rs分别表示投入和产出的松弛变量(投入的冗余量,产出的不足量),表示决策单元的效率值,m,s代表投入和产出的变量个数。
2.3 Tobit回归模型
Tobit 在 1958 年研究耐用消费品需求时提出的 Tobit 模型进行回归分析。把相关影响因素作为自变量,因变量为 DEA 交叉效率值,建立了 Tobit回归模型。具体模型如下:
(4)
式(4)中X为自变量向,Y为截断因变量,a为截距项向量,b为未知参数向量,扰动项ε~N(0,σ2)。这样可以通过显著性检验来检验该因素是否对效率值有显著性影响,并且可以通过系数来判断影响的大小和方向。
本文采用极大似然法估计Tobit参数,将第一阶段 SE-SBM-DEA 模型得到的效率值作为第二阶段 Tobit回归模型的效率值,得到危险性及相关解释变量的关系,可以有效地验证选取的相关指标的有效性。
3 研究区风险评价体系
3.1 风险评价体系
本文参考齐信等(2012)建立的地质灾害风险评价系统及相关文献资料(Wong,1982;罗元华, 1998;Dai et al.,2002;马寅生等,2004;王璐,2023; 周萌等,2024),结合平谷区具体情况和 DEA 方法,将地质灾害的发生过程看成一个“投入-产出”系统,将诱发因素和孕灾环境作为输入指标,将灾害的发育特征作为输出指标,而效率值 θ 则代表着成灾效率,建立平谷区风险评价的三级指标体系。以致灾体与承载体为评价对象,危险性与易损性作为一级指标,其中危险性的输入指标包括诱发因子、孕灾环境,输出指标为灾害发育特征;易损性的输入指标为物质、经济、社会、环境,输出指标为危害特征。结合平谷区地质灾害的分布规律及发育特征,进而完成三级指标体系的建立。利用DEA方法开展危险性与易损性评价,通过风险评价矩阵开展风险评价及风险区划,进而建立了平谷区地质灾害风险评价体系(图3)。
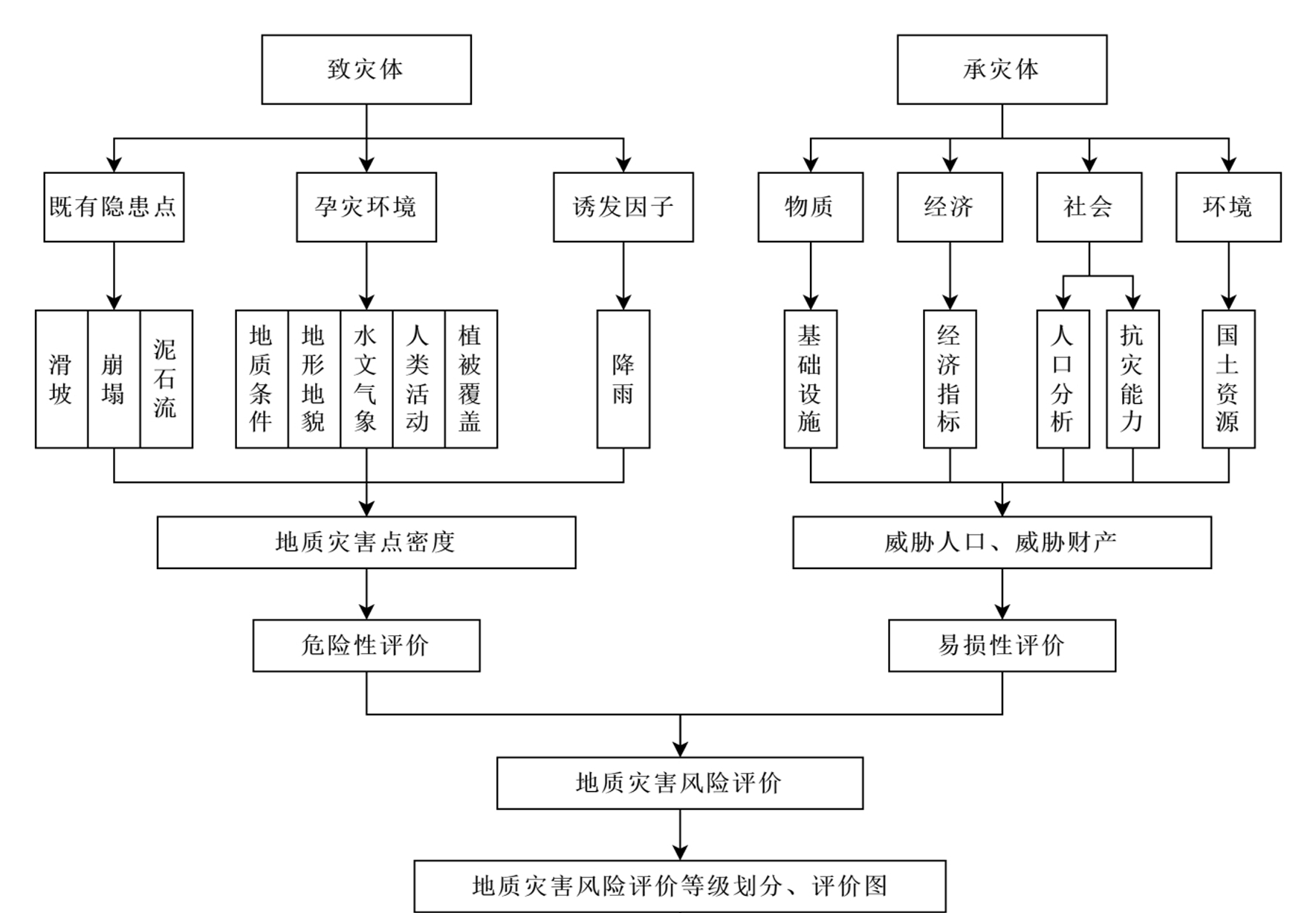
图3地质灾害风险评价系统
3.2 危险性评价
本文主要采用统计分析模型中的DEA-Tobit模型进行评价分析,相关数据来源于“北京市平谷区地质灾害风险普查”项目,数字化平台为 ArcGIS Desktop 10.0。使用数据主要包括地形地貌、地质构造、地层岩性、水文、降雨、植被覆盖指数、地质灾害信息。地形地貌来源于中国科学院计算机网络中心数据集;地质条件、地质构造参考 2004 年出版的 《中国地质图集》;地质灾害信息是参考平谷区风险普查项目获得;植被覆盖指数 NDVI 来源于地理空间数据云 2021年 Landsat8影像数据计算得到;降雨数据参照平谷区2016—2021年气象站降雨量数据,通过 ArcGIS 软件中的插值工具通过反距离权重法确定各栅格的降雨值;其他相关数据来自于“北京市平谷区地质灾害风险普查”项目。
区内以崩塌、滑坡、泥石流灾害点为主,根据其成灾机理不同,可以将崩塌滑坡划分为一类,其中评价单元为300 m×300 m格网;泥石流为一类,以流域为评价单元,由DEM数据进行提取划分。
根据其危险性分为 4 类:极高危险区、高危险区、中危险区、低危险区。在上述两类分别完成危险性划分后,利用GIS系统进行区域叠加,得到最终的危险性分区。
3.2.1 崩塌滑坡危险性评价指标体系
根据地质灾害的发育分布规律及地质条件,选取地质灾害现状及影响其发生发展的因子作为影响因素,现有 637 处崩塌滑坡隐患点。在搜集地质灾害发育分布情况的基础上,参考选择孕灾环境中的 9 个指标,包括坡度、坡向、起伏度、高程、工程地质岩组、到断层的距离、到河流的距离、植被覆盖率,诱发条件中的降雨指标,灾害点密度指标作为灾害特征,共计11个评价因子进行地质灾害危险性评价。在确定评价指标的基础上,根据不同评价指标结合研究区实际情况构建分级标准,具体分类情况如表1所示。
表1崩塌滑坡危险性评价因子分类说明

3.2.2 泥石流危险性评价指标体系
研究区开展过 1∶50000 泥石流精细化调查,现根据区内48条泥石流的精细化调查数据作为基础,以流域为评价单元,针对现有的48条泥石流沟进行危险性评价。考虑到DEA模型对数量的要求,基于现有数据进行了筛选,选择降雨作为诱发因子指标,选择纵坡降、主沟长度、流域面积、工程地质岩组、沿沟松散物储量、松散物平均厚度、断层数量、植被覆盖率共9个指标作为评价指标,一次性冲出量、峰值流量作为灾害发育特征指标,共计11个指标作为泥石流危险性评价指标,具体分类情况如表2所示。
3.2.3 基于 SE-SBM-DEA 模型的地质灾害危险性评价结果及分析
根据SE-SBM-DEA模型对危险性进行评价,具体思路是在地质灾害的危险性评价过程中,由诱发因素、孕灾环境共同作用下产生地质灾害,对平谷区崩塌滑坡、泥石流进行分类评价,确定了崩塌滑坡的 10 个输入指标(xij),1 个输出指标(yij),评价单元(DMU)10513个,评价单元面积 300*300 m²;泥石流 9 个,2 个输出指标,评价单元(DMU)48 个,以流域为评价单元。利用 ArcGIS 软件提取每个评价单元的输入指标、输出指标数据,模型选择MaxDEA X软件包络模型中的超效率(Andersen and Petersen, 1993)模型,将已建立的危险性评价指标体系中的分级数据按照指标体系中的输入和输出指标分别导入,运行后得到相应的效率值得出成灾效率。
表2泥石流危险性评价因子分类说明

某一评价单元的成灾效率 θ 越大,则代表着其危险性越高,因此可以利用成灾效率的对比进行危险性评价。将各项数据输入SE-SBM-DEA模型,得到其对应的成灾效率值并根据自然断点法得到相应的危险性分区,将崩塌滑坡评价单元分为4类(图4),对 48 条泥石流沟流域划分为 3 类(研究区其他区域成灾效率赋值为0,划分为低危险区)(图5),其危险性等级划分结果详见表3,其中极高危险区、高危险区灾害点分布占比均超过 85%,这表明此次危险性评价分区与现有灾害点分布情况相符。
在 GIS 平台下,将崩塌滑坡危险性评价结果与泥石流危险性评价结果进行叠加,将泥石流评价单元由流域转化为栅格,同时统一流域内危险性赋值相同,与崩塌滑坡危险性评价结果进行合并取算术平均值为最终的综合危险性分区结果。最后,利用 GIS 分析中的工具“Classical”将平谷区地质灾害风险结果分为 4 类:高危险区、中危险区、低危险区和低级危险区(图6)。综合来看,平谷区极高危险区及高危险区主要分布在平谷区北侧及西侧山区,其自然地理条件与地质环境背景为地质灾害隐患的发生提供了有利条件,现有分区结果与灾害点分布一致,符合客观规律与地质工程的评价结果(表4),同时根据结果可以看到在极高危险区和高危险区的现有地质灾害隐患点582个,占比约85%,这表明此次危险性评价分区与现有灾害点分布情况及孕灾条件相符。
表3危险性等级划分
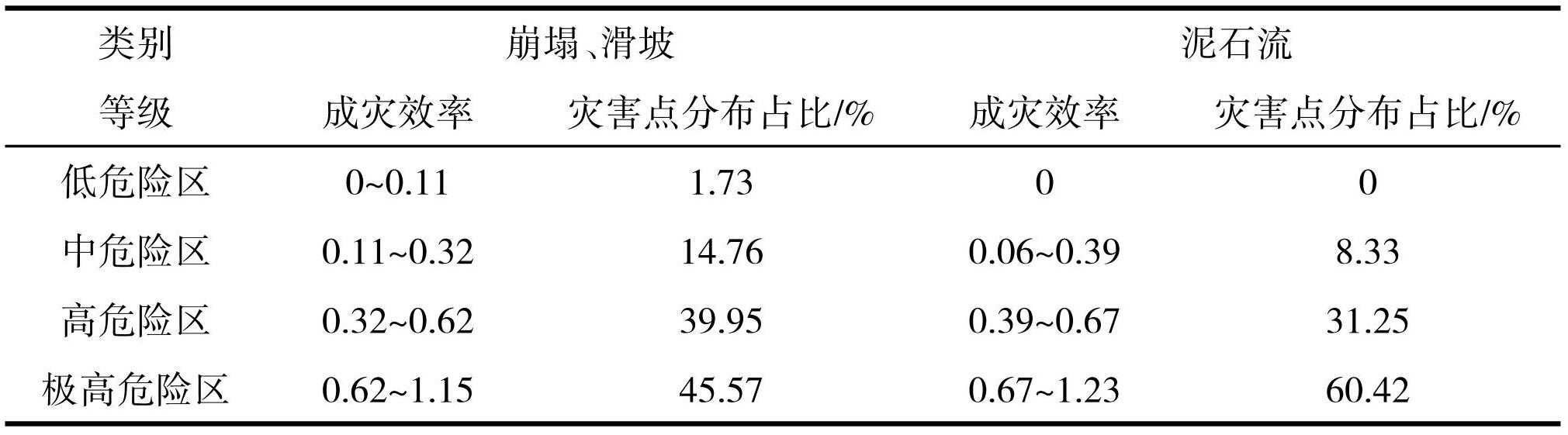
表4平谷区地质灾害危险性评价分区说明


图4崩塌滑坡危险性分区图

图5泥石流危险性分区图

图6平谷区危险性综合示意图
3.2.4 基于 Tobit 回归模型的危险性分区影响因素分析
按上述的地质灾害危险性评价体系,应用Tobit 模型针对上述评价指标体系的危险性影响因素进行分析。由于泥石流危险性评价仅有48个数据单元,数据量有限,故本文不进行Tobit回归分析。崩塌滑坡危险性评价单元为 10514 个,利用 SE-SBM-DEA 模型计算每个栅格区域的成灾效率,对其进行Tobit 模型回归分析。解释变量为坡度、坡向、起伏度、高程、工程地质岩组、到断层的距离、到河流的距离、植被覆盖率,诱发条件中的降雨指标,使用 SE-SBM-DEA模型的效率值作为因变量,创建了Tobit线性回归模型,利用 R 语言软件的计算结果如表5所示。结果显示,其中岩组、降雨对危险性影响较大,其他影响因素也均都通过了显著性检验,表明本文选择的评价因子对危险性有很强的影响力,表明本文选取的地质灾害危险性评价因子是合理的,其评价结果在一定程度上是符合统计学规律的。
3.3 易损性评价
3.3.1 易损性评价指标体系的建立
易损性主要是承灾体属性的体现,主要是给定地区和时段内因潜在自然灾害可能导致的潜在总损失,风险分析中的后果分析。易损性指标包括承灾体属性指标和社会承灾能力指标,前者是指灾害载体的类型,包括自然属性、经济属性、社会属性等,而后者相对抽象,难以量化,例如抗灾能力,与承灾标准和及时性相关(Alcantara-ayala,2002)。相较于危险性评估,易损性评价的难点在于承灾体的界定及其易损性定量评价方法,大多数是通过遥感结合调查统计进行整合和处理(刘兰芳和何曙光,2006;张桂荣等,2007;Pandey et al.,2010)。本文采用DEA-CCR模型进行易损性评价,以2022年平谷区统计年鉴和“北京市平谷区地质灾害风险普查”项目为基础,以乡镇行政区作为评价单元,选取相应的物质、经济、社会、环境易损性输入指标,选取威胁人口与财产作为输出指标,共7个评价因子,详见表6。
3.3.2 基于DEA-CCR模型的地质灾害易损性评价结果及分析
本文采用 DEA-CCR 模型开展承灾体的易损性评价,具体思路是在评价过程中,区域的经济、物质、社会、环境等因素决定着承灾体在外界环境下的暴露程度,而灾害发育特征作为承灾体的受损情况,暴露情况越突出,则承灾体的受损情况可能越严重。因此将经济、物质、社会、环境等现状因素作为 5 个输入指标(xij),灾害危险特征 2 个输出指标 (yij),评价单元(DMU)14个,以乡镇行政区划为评价单元。利用统计数据,模型选择 MaxDEA X 软件包络模型中的径向CCR模型,将已建立的易损性评价指标体系中的分级数据按照指标体系中的输入和输出指标分别导入,运行后得到相应的效率值 θ。利用效率值 θ 对比进行易损性评价,某一评价单元的效率值θ越大,则代表着其易损性越高,具体评价结果见表7。
依据自然断点法得到相应的易损性分区,划分为4类(表8),根据地质灾害易损性评价分区图可知 (图7),其中镇罗营与熊儿寨为极高易损区,大华山与金海湖为高易损区,其他区域易损性相对较低。

图7地质灾害易损性评价分区图
表5崩塌滑坡Tobit回归分析

注:***、**、*分别表示在0.01、0.05、0.1水平上显著相关。
表6易损性评价因子分类说明

表7地质灾害易损性评价结果一览

表8地质灾害易损性分区说明

3.4 地质灾害风险评价
地质灾害风险性评价是在危险性和易损性评价的基础上进行的,其主要评价思想是:根据地质灾害危险程度,结合地质灾害中承灾对象可能遭受地质灾害破坏的严重程度,对地质灾害致灾体与承灾对象遭遇的地质灾害风险进行客观评价。本文采用矩阵分析方法(表9)将地质灾害的危险性和易损性评价结果叠加运算,划分为地质灾害极高风险、高风险、中风险及低风险。风险区划在风险评价结果的基础上,通过消除零碎图斑等除燥处理,并根据近似性原则,将评价区划分成 4 个风险等级 (图8),共有 4 个极高风险地区,8 个高风险地区,5 个中风险地区,1 个低风险地区(表10)。根据风险评价结果可以得出,其中极高风险区及高风险区包括了 591 个地质灾害隐患点,占总地质灾害点的 86.3%,风险区划结果与地质灾害点分布相符。

图8平谷区地质灾害风险等级评价区划示意图
根据以上风险评价结果,可以结合地区规划与要求,进一步提出有针对性的地质灾害防治规划,将地质灾害防治区域划分出重点、次重点和一般共 3 类地质灾害防治分区(表10),根据分区结果分别采取工程治理、搬迁避让、监测预警等一种或多种风险管控建议,进一步完善风险管理体系,最大程度上降低地质灾害风险,提高防治效益,为平谷区的防灾减灾相关工作提供参考。
表9地质灾害风险等级划分建议

表10平谷区地质灾害风险评价分区说明

4 结论
根据平谷区地质灾害发育特征及危害特征,基于 GIS 平台处理致灾体与承载体基础数据,构建 DEA模型开展风险评价,得出以下结论:
(1)研究区对于致灾体按照历史灾情、孕灾环境、诱发因子等成因机理和危害特征确定了崩塌滑坡和泥石流 2 类各 11 个危险性评价因子,利用 SE-SBM-DEA 模型开展危险性评价与分析,其极高危险区、高危险区面积占比 23.5%,灾害点占比 84.09%,主要分布在平谷区北部—东部山区;按照承灾体类型及抗灾能力确定了物质、经济、社会、环境和危害特征共 7 个易损性评价指标,利用 DEA-CCR模型开展易损性评价与分析,其中镇罗营与熊儿寨为极高易损区,大华山与金海湖为高易损区,其他区域易损性相对较低。
(2)根据本文风险评价结果,研究区共有4个极高风险地区,8 个高风险地区,极高风险区、高危险性区域占全区面积的 27.63%,主要位于镇罗营、大华山、金海湖等北部、东部地区山区,其分布地质灾害点 591处,仅占总灾害点数量的 86.3%,地质灾害发育程度高,危害程度大,其地质灾害分布情况与风险区分布情况相符。区内不宜开展大规模城镇和工程建设,建议将人口及相关经济体有序向低危险区引导,针对现有地质灾害点主要采用工程治理、搬迁避让、监测预警等多种风险管控措施相结合的手段开展防治工作。
(3)本文通过利用DEA方法中的SE-SBM-DEA 模型和 DEA-CCR模型分别开展危险性评价与易损性评价,相关指标为自然属性和社会经济属性的客观数据,无需进行量纲处理与权重假设,利用 Tobit 模型对得出的评价结果进行回归分析,可以避免变量之间的多重共线性,验证选取的相关指标的有效性,综合来看DEA方法极大地提高了风险评价工作的效率。
(4)本文将统计学中的DEA方法应用在地质灾害风险评价中,建立了基于DEA方法的地质灾害风险评价体系,提供了DEA方法在地质灾害风险评价中的有效应用,也为平谷区的地质灾害地灾预警与防护工作提供有效的科学依据。同时受现阶段数据及研究现状影响,本文也存在一定的局限性,一是易损性指标体系的建立仍需不断完善;二是 DEA方法对数据异常值较为敏感,异常值可能会影响生产前沿面的构建和效率值的计算,后续研究中可进行分级赋权处理在一定程度上降低了异常值的影响;三是 DEA 和 Tobit 模型在不同数据规模的应用上有所差异,在较大规模数据基础上应用更有优势,因此在后续的研究中可根据数据精度情况寻找最合适的评价单元,评价单元越小,数量规模越大,其方法应用更有效。

















