摘要
在钻探过程中,存在钻孔轨迹偏离预定目标和岩心取样不完整或失真问题,导致钻探偏差变化率较大,修正效果不佳。为此,提出基于改进密集轨迹算法的不同地质岩心钻探偏差修正。采用卸压平衡原理,针对不同地质岩心条件确定了有效的钻孔深度,探究钻探方位角,引入改进密集轨迹算法,构造多尺度金字塔,并计算每个数据点的自相关矩阵特征值,结合钻探影响域构造钻探控制域,采用贝叶斯共轭分布理论整合先验信息和实际数据,对照不同控制域地质岩心钻探数据的密度函数,分析钻探钻进速度与泥浆压力梯度之间的关系,调整钻探倾角,对不同地质岩心钻探偏差进行修正。算例实验结果显示,采用本文所提出的方法后,钻探偏差变化率明显降低,偏差修正效果得到了显著提升。该方法有效实现了偏差的最小化,并最大化了修正效果,从而提高了地质勘探的精度和效率。
Abstract
During drilling operations, issues such as deviation of the borehole trajectory from the intended tar‐get and incomplete or distorted core sampling occur, leading to significant variations in drilling deviation rates and suboptimal correction outcomes. Therefore, a correction of drilling deviation in different geological rock cores based on improved dense trajectory algorithm is proposed. By applying the principle of pressure relief equilibrium, effective drilling depths were determined for different geological core conditions. The drilling azimuth was investigated, and an improved dense trajectory algorithm was introduced to construct a multi-scale pyramid. Constructed a multi-scale pyramid, and calculated the eigenvalues of the autocorrelation matrix for each data point. By integrating the drilling influence zone with the constructed drilling control zone using Bayesian conjugate distribution theory to combine prior information and actual data, we compared the density functions of geological core drilling data across different control zones. This analysis examined the relationship between drilling penetration rate and mud pressure gradient, and the drilling inclination angle was adjusted to correct drilling deviations for different geological cores. The experimental results demonstrate that the method proposed in this article, the rate of change in drilling deviation is significantly reduced, and the effect of deviation correction is significantly improved. This method effectively minimizes the deviation and maximizes the correction effect, thereby improving the accuracy and efficiency of geological exploration.
0 引言
在地质勘探领域,岩心钻探是一项至关重要的技术,其准确性和精度直接关系到地下资源的有效开发和地质研究的深化。然而,在实际钻探过程中,由于地层的复杂性、钻探设备的局限性和环境因素,钻孔偏移问题难以避免。不同地质岩心钻探,指的是在钻探过程中,面对不同种类、性质和结构的岩石层,需要采用不同的钻探工艺、方法和设备口径。例如,在坚硬且完整的岩石层中,可能需要使用大口径的钻头以加快钻探速度;而在松散、破碎的岩石层中,则需要使用小口径的钻头以确保岩心取样的完整性和准确性。传统的勘测技术在面对复杂地层和恶劣环境条件时,往往效率低下且校正精度难以保证。随着技术的发展,特别是自动化和智能化技术的不断进步,为钻井纠偏提供了新的解决方案。
赖林峰(2023)提出一种通过钻取代表性地质岩心的方法,旨在确保岩心能够真实反映地层内部质量。通过对比分析计算得到的回弹值与岩心强度值,建立了回弹值与抗压强度的关系模型,进而实现了对钻探回弹值的精确修正。该方法适用于大规模地质岩心的快速、高效钻探评估与修正,能够提升工作效率并降低成本。然而,钻探设备的操作和岩心取心过程可能存在人为误差,如岩心取样不完整或失真,这些因素可能影响到校正结果的准确性。赵家忠(2021)通过在钻井设备的关键部位安装光纤传感器,实时采集钻探数据,并基于数据处理结果控制系统生成相应的控制指令,以调整钻探参数,实现对钻探偏差的精准修正。该方法提高了钻孔精度,但光纤传感器及相关设备的成本较高,增加了钻井作业的总成本。 Mamane et al. (2022)依据实际钻井过程,建立了高精度的数值模型。通过分析数值实验结果,该方法能够识别和量化钻井过程中可能出现的误差,并利用数值修正算法对钻探误差进行实时校正,提高了钻孔结果的准确性。然而,该方法的性能高度依赖于实时监测数据的质量和完整性,任何数据错误或缺失都可能影响钻孔轨迹,导致偏离预定目标。Liang et al.(2023) 针对钻井作业的具体需求和条件,利用管道黏度计实时收集钻探数据,提取与钻井参数相关的特征信息,并根据数据分析结果校准钻探参数,如钻头速度和进给压力,以确保钻井过程的稳定性和效率。该方法实现了数据的实时收集与处理,能够及时发现并纠正钻井参数的变化。然而,粘度数据与钻井参数之间的关系可能复杂,需要专业知识和经验进行准确解释和处理,这可能导致钻探偏差变化率相对较大。
针对现有方法的不足之处,本文结合改进密集轨迹算法对不同地质岩心钻探偏差进行修正,旨在提高钻井作业的效率和质量,也为合理开发地质资源和深入开展地质研究提供了有力支撑。
1 不同地质岩心钻探偏差修正方法设计
1.1 基于改进密集轨迹算法的钻探偏差角度计算
在实际工程应用中,地质岩心钻探偏差修正需要根据钻探角度来进行,通过有效的修正可以使钻探路径回归到预设的轨迹上,提高钻探的精度和效率。因此,钻探偏差角度计算是偏差修正的前提和基础,而偏差修正是确保钻探按照预定角度进行的必要手段(冯美贵等,2023)。
在地质岩心钻探过程中,采用卸压平衡原理计算地质岩心在受力时的平衡方程,表达式如下:
(1)
式(1)中,α0 表示卸压区边界效应力(Pa);r0 表示应力集中区的剪切应力(Pa);we表示比例系数;Ac 表示叠加标度函数。
为了更好地分析确定不同地质岩心下的有效钻孔长度,取有效钻探投影下轴线上的长度为有效钻孔宽度,钻孔与轴线的偏角为方位角(刘云飞等, 2023),具体如图1所示。
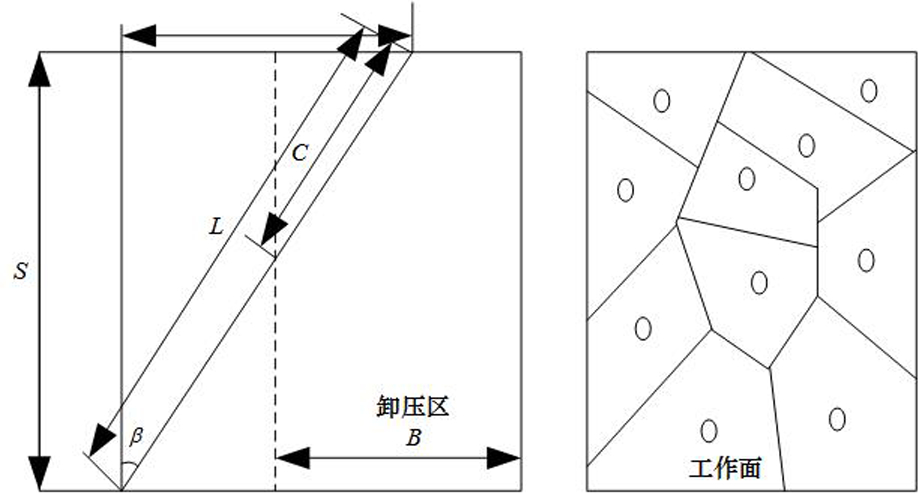
图1钻探示意图
图1中,S表示钻探深度在工作面上的投影长度 (m);L表示实际钻探深度(m);B表示工作面前方卸压区宽度(m);C表示有效钻孔长度(m);β表示钻探方位角(°)。依据上图,可计算得到钻探方位角偏差值为:
(2)
式(2)中,za表示钻探俯仰角(°);gb表示系数矩阵。
采用改进密集轨迹算法在钻探数据中构造多尺度金字塔,并计算每个数据点的自相关矩阵特征值(张蒙蒙等,2022),表达式为:
(3)
式(3)中,f0 表示密集光流场(m/s);kj 表示光流的水平分量(m/s);lc表示特征点的运动方向(°)。
对钻探平面数据的位移矢量进行正则化操作,即可得到钻探轨迹特征描述子(谭春亮等,2023),计算公式为:
(4)
式(4)中,χ0表示正则化因子;Xb表示运动显著性差异系数。
由此可得到钻探轨迹的偏移特征向量,即:
(5)
式(5)中,jc表示光流直方图;v0表示描述符长度 (m);Wk表示规范性常数。
进而可采用下式确定钻探偏差角度,即:
(6)
式(6)中,φk表示偏差度函数;n0表示数据量;sd 表示距离权值。
依据卸压平衡原理分析钻探过程中的受力情况,结合钻探方位角偏差,采用改进密集轨迹算法提取钻探轨迹特征,从而确定钻探偏差角度,为接下来构建地质岩心钻探控制域打下基础。
1.2 构建地质岩心钻探控制域
地质岩心控制域是一个预设的空间范围,定义了钻探作业的安全边界与预期目标(李彩虹等, 2021)。在这个控制域内,钻探作业应该按照预设的轨迹和参数进行,由此,整理钻探偏差角度,确认岩心钻探控制域,以确保钻探的准确性和安全性。
获取钻探工作面的钻探数据和地平面数据,并将两种数据进行合并,从而计算散点数据的高度值 (金鑫,2023),即:
(7)
式(7)中,θz 表示钻探角度(°);η0 表示截断误差;γt表示信任函数。
接下来计算钻探数据与地质平面数据之间的关联性(王修昌等,2021),即:
(8)
式(8)中,Dt表示值域;yf表示朗德因子;mk表示相关性系数。
依据数据间的相关性,对数据进行分组,结合分组单元和相邻电源中的离散点分类结果计算数据熵值(高辉等,2023),表达式如下:
(9)
式(9)中,pk 表示分组后各级单元出现的概率; ec 表示索引因子;ω0 表示属性约束;mf 表示判别误差。
由此利用钻探影响域确定钻探偏差修正的控制域(郭达等,2023),表达式如下:
(10)
式(10)中,at 表示线性常数;Us 表示分辨系数; ht 表示一阶滞后变量;Pn 表示影响域函数;ς1、ς2 分别表示钻探控制域的上限与下限。
基于钻探角度,采集钻探数据与地面数据(姜杰等,2023),并计算两类数据之间的相关性,结合钻探影响域构造钻探控制域,为后续实现钻探偏差修正提供便利条件。
1.3 钻探偏差修正
当岩心钻探控制域数据有限或不确定时,采用贝叶斯共轭分布理论整合先验信息和实际数据来获得更准确的后验概率分布,从而获取不同地质岩心钻探数据的密度函数,以更好地理解和描述地质岩心的特征(谢春临等,2021)。
(11)
式(11)中,kl表示观测样本;vd表示地质局部孔隙压力(Pa);ς1、ς2分别表示钻探控制域的上限与下限(m)。
基于上式得出钻探钻进速度与压力梯度之间的关系为(高晓亮,2023):
(12)
式(12)中,μ0表示钻探动力方程系数;表示压力梯度。
由此可调整钻探倾角(梁铭等,2023),即:
(13)
式(13)中,xt 表示预定的目标方位角(º);Cy 表示状态矩阵;υd表示经验常数(巩泽文,2023)。
进一步可采用下式完成对不同地质岩心钻探偏差的修正,即:
(14)
式(14)中,gm 表示岩心颗粒级配(孙川翔等, 2023);ψk表示线性函数;表示偏差修正结果。
根据地质岩心的颗粒级配确定岩心类型,进而利用上式对不同地质岩心钻探偏差进行修正,使得钻探路径符合预设轨迹,保证钻探效率(刘伟吉等, 2023)。
2 算例论证
为验证本文设计的改进密集轨迹算法的不同地质岩心钻探偏差修正方法在实际应用中的效果,将本文方法应用在某地质勘探作业中,并对其进行钻探偏差修正,设计算例实验。
使用 C#+ArcGIS Engline 进行实验环境开发,将其应用于某地区中进行地质岩心钻探。该地区的地质钻探现场图与岩层分布情况如图2所示。

图2地质钻探现场图(a)与岩层分布情况(b)
通过地质勘察,结合遥感图像的解释,对土壤地质地图和初步钻探数据的分析,对领土结构的稳定性和地质不良(如断层,滑体)进行特殊调查。钻井区各种岩石的厚度、空间分布和技术地质特性得到了相关数据。确定钻探区域的地质岩性如表1所示。
表1地质岩性

选用具有高精度定位功能的 XY-1 型钻机,设置钻孔深度为50 m,根据地层岩性和钻头类型设置钻孔速度为1 m/h;根据地质变化和实验要求设置采样间隔为 10 m/次,确保钻孔过程的稳定性和准确性。
采用 DTM-352C 系列全站仪、DT510 型电子经纬仪测量钻孔位置、角度等参数;采用 SPSS、Excel 数据处理软件对实验数据进行处理和分析。
对不同地质岩心条件下的钻探数据进行统计,并系统分析岩石差异对钻探法规的影响。检测每个钻孔深度范围和颗粒分层,样品编号,颗粒分布等。对偏差角度和钻进过程中的工况变化进行记录。确保统计数据完整覆盖岩性转换关键节点,为后续偏差修正效果验证提供数据支撑。不同岩心下的钻探数据如表2所示。
表2不同岩心下的钻探数据
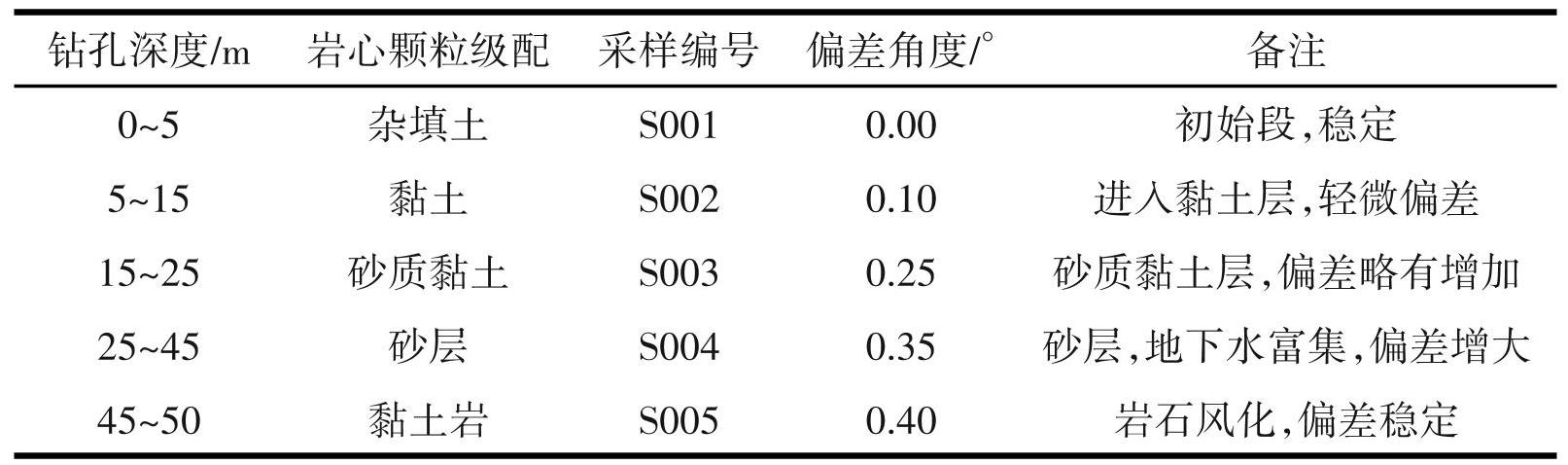
设置改进密集轨迹算法的相关参数如下。采样间隔pc = 5F,特征点领域大小5*5px,平滑滤波器尺寸 3 × 3,特征点阈值 κ = 0.5,梯度强度 j = 0.01,轨迹长度阈值G = 6F,最大位移S = 3px。
选取当前较为成熟的成矿钻探偏差修正方法作为对照组方法,本文方法作为实验方法,并基于实验结果分析不同方法的实际应用性能。
将本文方法应用于图2所示的钻探偏差修正中,并引入数值模拟方法(方法 1)、图像识别算法 (方法 2)作为本文方法的对比方法。分别采用 3种方法对该地质岩心钻探偏差进行修正,比较不同方法修正后的钻探偏差变化率,从而分析不同方法的修正效果,实验结果如图3所示。

图3钻探偏差修正结果
由图3可知,应用本文方法对地质岩心钻探偏差进行修正,得到的钻探偏差变化率明显低于方法 1 和方法 2,证明了本文方法的有效性,因为结合钻探方位角偏差,结合钻探数据与地面数据,计算两类数据之间的相关性,并构造钻探控制域,根据地质岩心的颗粒级配确定岩心类型,进而对不同地质岩心的钻探偏差进行修正,具有更加优异的性能。
采用钻孔轨迹平滑度作为评估不同方法修正性能的指标。钻孔轨迹平滑度越高,表明实际钻探路径与预设路径越一致,钻探偏差修正效果越好,对比结果如图4所示。

图4基于不同方法的钻探轨迹平滑度结果
由图4可知,在所研究方法的应用下,钻孔轨迹平滑度远高于对照组方法,在不同钻探偏差角度下,本文方法的钻孔轨迹平滑度始终控制在50%以上。因为本文方法依据卸压平衡原理,采用改进密集轨迹算法提取钻探轨迹特征,分析钻探过程中的受力情况,从而确定钻探偏差角度,可以更好地修正钻探偏差,修正性能更佳。
3 结束语
(1)本研究针对钻探过程中的偏差问题,提出了基于改进密集轨迹算法的修正方法。
(2)通过结合地质岩心特性、卸压平衡原理和方位角控制,构建多尺度金字塔框架,并计算数据点的自相关矩阵特征值;利用钻探影响域构建控制域,并引入贝叶斯共轭分布理论整合先验数据和实时数据,分析钻进速度与泥浆压力梯度的关系,从而实现对钻探偏差的有效修正。
(3)采用本研究的改进密集轨迹算法后,钻探偏差变化率大幅下降,轨迹平滑度和准确性显著提高。该方法通过对照不同控制域数据的密度函数,更精准地调整钻探倾角,有效修正了不同地质岩心的钻探偏差。
(4)本研究不仅优化了钻探过程,提高了勘探精度和效率,还扩展了密集轨迹算法和贝叶斯共轭分布理论在地质勘探领域的应用,为相关研究提供了新思路。





