摘要
为解决复杂地质条件下隧道突涌水量预测精度低与计算繁琐的问题,本文基于经典水文学原理,建立了一种适用于不同水文地质条件的隧道涌水量半解析计算模型。模型通过将有界含水层转化为无界恒定流问题,并结合叠加原理与卷积积分方法推导出涌水量随时间变化的理论表达式。采用本文模型,系统分析了渗透系数、含水层厚度、贮水率、隧道半径及初始水位等关键参数对隧道涌水量的敏感性。最后依托两个典型隧道涌水案例与本文方法结果进行对比验证。结果表明:隧道涌水量与渗透系数成正比;含水层越厚,储水量越大,涌水量达到稳定所需的时间越长;与其他参数相比,贮水率对涌水量的影响不显著; 实测隧道涌水量与模型计算结果吻合度较高,证明本文方法可行。研究结果不仅对隧道涌水量的预测具有一定参考意义,而且可根据实测涌水量反算现场水文地质参数。
Abstract
To address the challenges of low prediction accuracy and computational complexity in forecasting tunnel water surges under complex geological conditions, this study presents a semi-analytical model for tunnel inflow applicable to a wide range of hydrogeological settings. The model transforms a bounded aquifer into an equivalent unbounded steady-flow problem and employs the superposition principle together with convolution integrals to derive a closed-form time-dependent expression for inflow. Based on this formulation, a parametric sensitivity analysis is conducted to examine the effects of hydraulic conductivity, aquifer thickness, specific yield, tunnel radius, and initial head on inflow evolution. The validity of the model is further evaluated through comparison with measured inflow data from two representative tunnel cases. Results indicate that inflow is proportional to hydraulic conductivity; a larger aquifer thickness increases storage capacity and prolongs the time required to approach quasi-steady conditions; compared to other parameters, specific yield exerts a relatively minor influence; and the model’s predicted inflow agrees closely with observed values. These outcomes verify the feasibility and reliability of the proposed method. The developed semi-analytical model not only offers an effective tool for predicting tunnel inflow under diverse geological conditions, but also enables inverse estimation of in situ hydrogeological parameters from measured inflow data.
Keywords
0 引言
隧道突涌水问题是隧道工程所面临的巨大挑战之一(房忠栋等,2021;乔彤等,2023;周家兴等, 2024)。中国西南山区岩溶作用强烈,地下形成大规模溶蚀空腔及地下暗河通道,隧道开挖过程中,暗河一旦被揭露,可能会造成大规模隧道突水事故 (黄鑫等,2018)。此外,受断裂构造影响,隧道在穿越富水断层同样会引发隧道突水、突泥灾害,造成重大人员财产损失。因此,隧道开挖后涌水量的计算与预测,对隧道安全施工及运营具有重要工程指导意义(王德明等,2018)。
针对隧道涌水机理及涌水量理论模型方面,Go‐ lian et al.(2021)研究了高压富水溶洞涌水致灾机理,提出了确定隧道涌水量计算的数学模型。刘世伟等(2018)给出了4种不同透水边界下隧道涌水量计算方法。李林毅等(2018)依托深埋式中心水沟排水隧道,采用理论方法推导了半无限平面内隧道渗流场及涌水量解析解。曾凡祥等(2022)和杨闪等(2023)采用比拟法预测了岩溶矿坑涌水量,研究结果可为矿山涌水量计算及防排水系统设计提供重要参数;在物理模型试验方面,李铮等(2016)采用隧道渗流模型试验研究了注浆圈或初衬渗透系数对隧道涌水量影响。吴昊等(2017)研究了断层破碎带对隧道涌水影响。结果表明,地表水补给可显著增加隧道涌水可能性;数值模拟方面,黄震等 (2019)研究了充填型岩溶隧道突涌水运动特征,建立了岩溶管道滑移失稳突水的地质模型和力学传递模型。郭晓亮和高乐(2015)采用 FLAC3D研究了隧道开挖后地应力释放对涌水的影响。周宗青等 (2020)采用DEM-CFD耦合方法开展了隧道突涌水机制研究,提出了变强度-变渗透性-变黏度的渗透破坏机制。
综上所述,关于隧道涌水量研究已经取得了重要进展,但数值方法应用烦琐且耗时,而模型试验由于尺寸较小且试验材料无法与实际情况相同,所得到的结果具有局限性。与数值方法和模型试验相比,理论解析法具有方便快捷的优点。为此,本文首先基于经典水文学原理,提出了一种半解析方法,并对模型中的关键特征参数进行敏感性分析,最后与工程案例进行对比分析,验证本文理论的合理性。

图1隧道附近水位下降
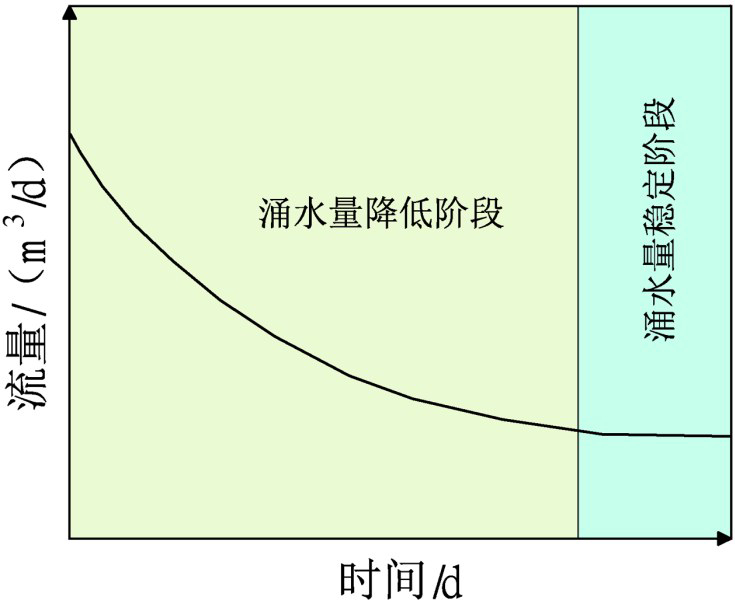
图2隧道涌水量随时间变化规律
1 半解析理论
1.1 基本假设与模型构建
计算隧道涌水量时需将有界含水层转化为无界问题,时变流问题转化为恒定流问题,并结合叠加原理,采用卷积法求解。在进行数学模型构建时,需做以下假设:
(1)考虑推导过程的方便性,本文假定围岩均质且各向同性,岩体渗透系数为常数;(2)涌水量随时间变化满足先减小后稳定的规律,即隧道涌水量简化为随时间变化的方程;(3)忽略隧道涌水过程中沿隧道轴向补给,潜水流假定为一维流;(4)流体具有不可压缩性;(5)假定含水层满足等厚、均质、各向同性和无限延伸的条件。
对于任意水流时刻,含水层水头从初始地下水位下降到隧道涌水点水位(图1)。随时间的增大,涌水量逐渐减小,当涌水时间足够长,涌水量逐渐趋于稳定(图2)。因此,隧道涌水量可简化为随时间变化的方程。本文基于隧道涌水量随时间变化特征,提出一种简化模型,模型推导过程如下:
1.2 控制方程
对于恒定流量和变降深汇源项,控制方程可写成:
(1)
式(1)中,W 为水头降深(m),Q 为涌水量(m3 / s),χ为水头降深函数,P是水文地质学特征参数(如渗透系数、储水系数和含水层厚度等),r 是距涌水点的距离(m),t是涌水时间(s)。
根据卷积积分原理,相应水流变化解为:
(2)
式(2)中,Q0为初始涌水量(m3 /s),τ为时间间隔 (s)。
在进行数值积分时,进行离散化处理,公式(2) 可写为:
(3)
式(3)中,W(r,ti)为ti时刻的水头降深(m)。
若隧道进水点水头降深已知,式(3)可转化为:
(4)
式(4)中,Q为隧道口或隧道侧壁涌水量(m3 /s), H为常水头到隧道中心线的距离(m),r0为隧道半径 (m)。
根据初始时刻t=0,Q(t0)=0,进一步代入式(4)得到任意时刻隧道涌水量:
(5)
式(5)中,Q(t1)为任意时刻隧道口或隧道侧壁的涌水量(m3 /s),其他符号与前文相同。
1.3 水头降深函数
根据式(4),水头降深函数是涌水量计算的主要控制因素,不同水文地质参数存在不同的函数形式。根据Carslaw et al.(1962)的研究结果:
(6)
式(6)中,k 为含水层平均渗透率(m/s),λ 为含水层水力扩散系数(m2 /s),λ=k/s,s为贮水率(1/m),Θ 为高斯误差函数。
(7)
式(7)中,x为任意变量,u为积分下限。
Theis(1935)根据模拟隧道侧壁涌水量,假定含水层满足等厚、均质、各向同性和无限延伸条件下,水头降深方程:
(8)
式(8)中,T为Theis井函数,。
由于式(7)和(8)属于无穷域理论解,因此必须根据水文地质边界条件,利用图像法和叠加原理转化为有限域问题(图3)。以含水层顶部平面为对称面,可以得到与真实隧道相一致的虚拟镜像隧道Q1,以含水层底部平面为对称面,得到虚拟镜像隧道P1。同理,以含水层顶部平面为对称面,由 Q1得出 Q1',同理得到虚拟镜像隧道P1'和Q1(″ 图4)。进一步采用图像对称叠加原理,得到隧道涌水量计算函数为:
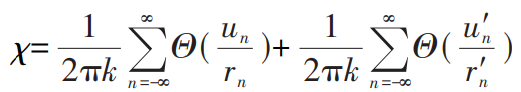
(9)
式(9)中,un=rn/(4λΔtij)1/2,rn=2nB,n为迭代次数,B 为含水层厚度(m),如果 n=0,rn=r0,则 u' n=r' n(4λΔtij) 1/2, r' n=(((2nBcosθ)2 +2D2)+(2nBsinθ) 2) 1/2。
式(9)的计算精度取决于序列项数量。图5显示了半径为 5.6 m 的隧道穿透厚度为 75 m 含水层,且初始水位下降200 m工况下的隧道涌水量。结果表明,当迭代项 n达到 20时,计算结果收敛。因此,工程计算前,应尽可能选择足够的迭代项,从而获得较高的精度。为此,本文定义收敛标准:
(10)
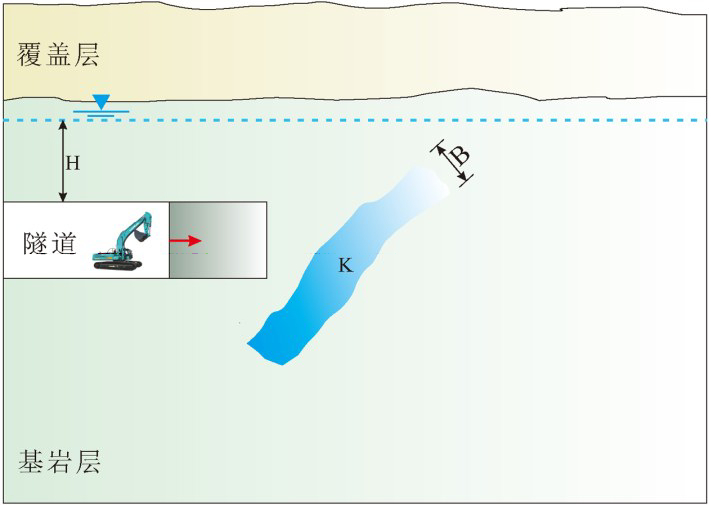
图3含水层与隧道相对位置示意图
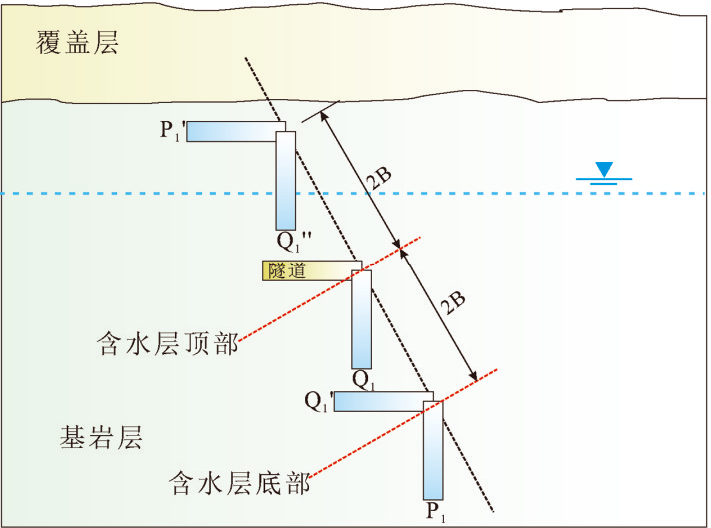
图4隧道涌水简化模型
式(10)中,Qn+1、Qn分别为利用第 n 项和第 n+1 项计算的涌水量。根据上述标准,迭代项 nc随含水层厚度B和倾角α的变化而变化(图6)。结果表明,倾角 α 对迭代项 nc的影响很小,但随着含水层厚度的减小,结果收敛所需的迭代项会显著增加。
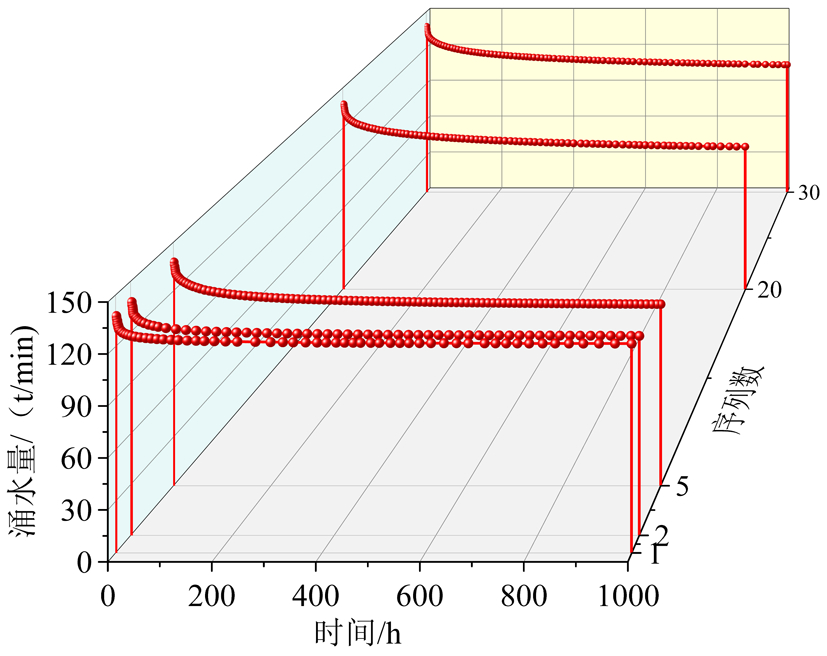
图5迭代次数对收敛的影响
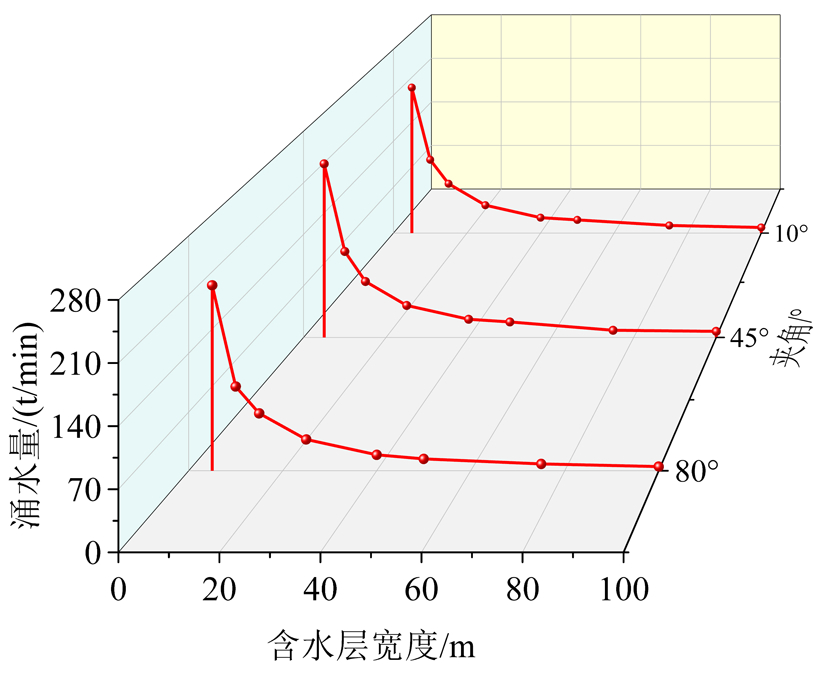
图6含水层倾角对涌水量的影响
2 参数敏感性讨论
图7显示了含水层不同渗透系数对隧道涌水量的影响。其中,含水层宽度为 70 m,贮水率为 0.0001 m-1。结果表明,隧道涌水量与渗透系数成正比。此外,在最初的4 h内,隧道涌水量急剧降低,随后隧道涌水量逐渐趋于稳态。由此可见,含水层渗透系数对隧道涌水量影响显著。根据图7,渗透系数增大或减小单位数量级,涌水量结果的相对误差非常显著。实际工程中,合理估算含水层渗透系数是准确计算隧道涌水量的重要指标。图8显示了含水层厚度对隧道涌水量影响。结果表明,当含水层宽度小于 10 m 时,涌水量随含水层厚度增加而增大,但含水层厚度大于 10 m 时,涌水量减小的速率变小,证明含水层越厚,储水量越大,消散时间越长。
根据式(5)与图9结果,在保持含水层渗透系数、宽度及隧道半径相同的情况下,隧道涌水量与初始水位成正比。进一步假定含水层渗透系数随深度增大而线性减小,得到渗透系数与初始水位联合作用对涌水量的影响如图10所示。结果表明,由于渗透系数和初始水位共同影响,隧道涌水量不一定随初始水位的增加而增大,证明含水层渗透系数随深度的变化规律对涌水量的计算同样比较关键。
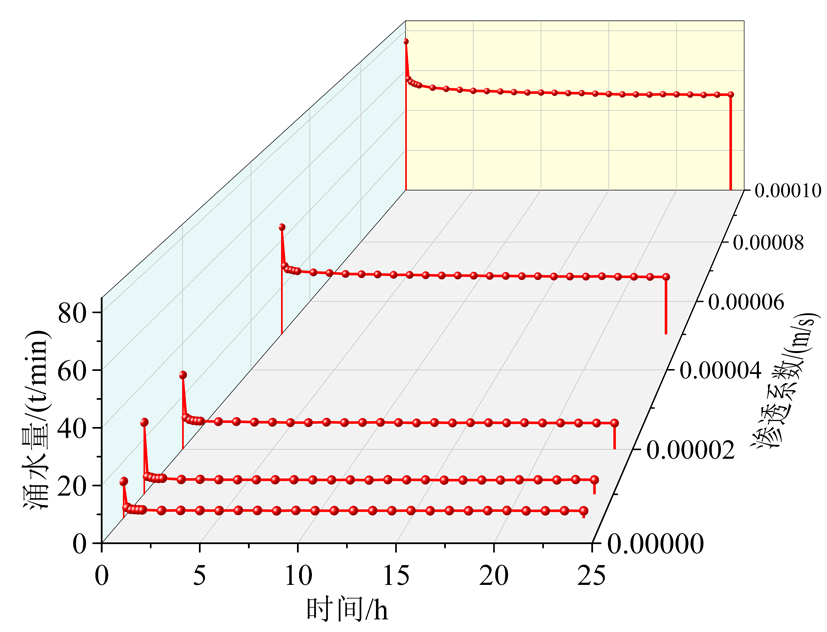
图7渗透系数对涌水量的影响

图8含水层宽度对涌水量的影响
图11给出了隧道半径对涌水量的影响。结果表明,涌水量随隧道半径增大而呈非线性增大趋势。图12显示了贮水率对隧道涌水量影响,与其他参数相比,贮水率对隧道涌水量的影响不显著。
根据以上分析,实际工程中若获取含水层厚度、渗透系数、贮水率、常水头到隧道中心线的距离以及隧道半径 5 个特征参数即可预测隧道涌水量。其中,渗透系数与隧道涌水量成正比,对隧道涌水量影响最大;含水层厚度和储水量的大小,会影响涌水量达到稳定所需的时长;隧道半径与涌水量的关系呈非线性规律,而贮水率对隧道涌水量影响不显著。
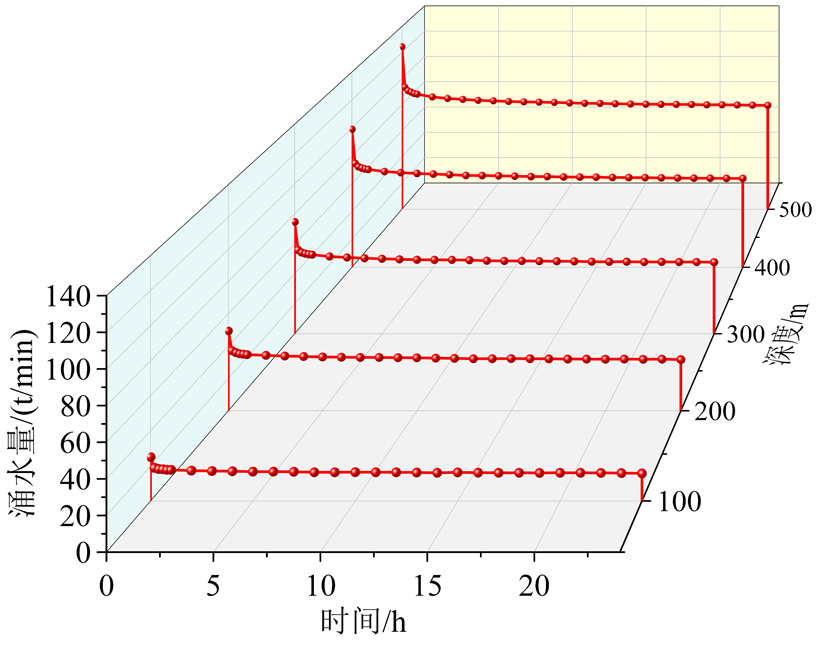
图9深度对涌水量的影响
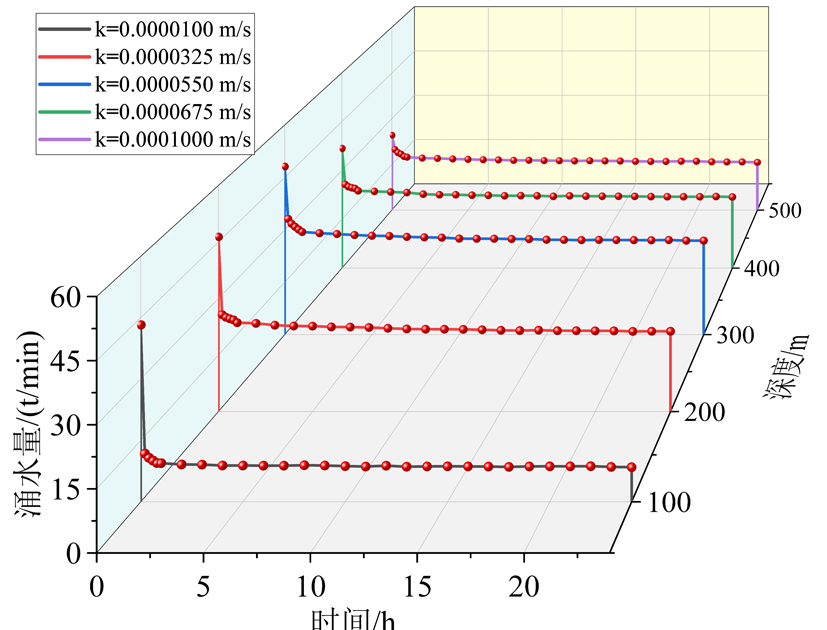
图10渗透系数与深度联合作用对涌水量的影响

图11隧道半径对涌水量的影响
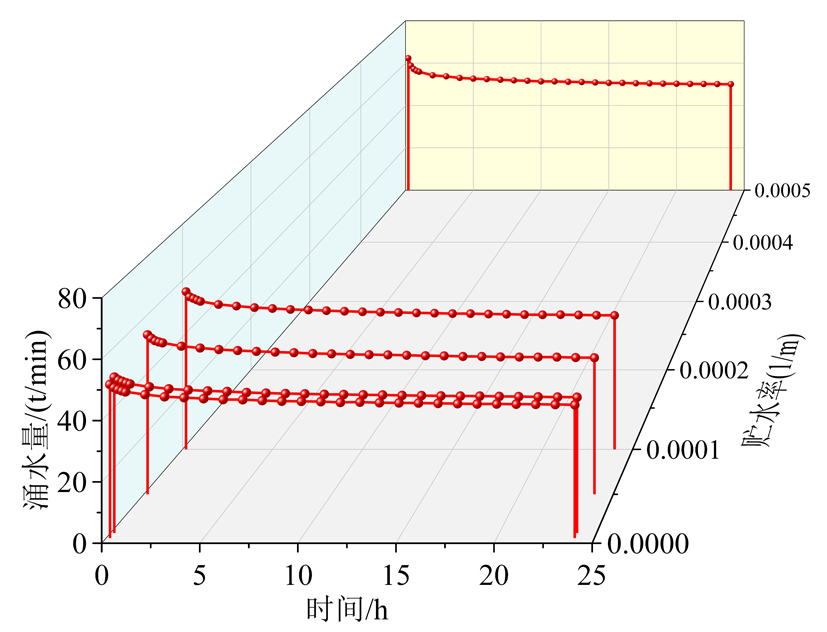
图12贮水率对涌水量的影响
3 工程案例验证
3.1 太子山隧道
太子山隧道位于湖北省荆门市境内。隧道全长 2100 m,最大埋深约 183 m,半径 5.4 m。隧道为单洞双线隧道,设计行车速度为 350 km/h。隧址区主要穿越碳酸盐岩及碎屑岩。其中,碳酸盐主要为二叠系、三叠系和石炭系灰岩,且隧道自东向西穿越太子山断裂和南漳—荆门断裂带等多条断裂带。区内地质构造发育,断裂构造走向多为北西向。由于隧道所在位置岩溶作用强烈,地下暗河发育。 2023年3—8月隧道施工期间多次遇到涌突水灾害,严重影响隧道的安全施工(图13)。
根据开挖后太子山隧道涌水量观测统计,在 DK124+882 隧道进口上台阶左边墙拱脚处存在大型溶洞和地下暗河含水层,施工期间出现涌水和渗水现象,属于典型地下暗河型突水。现场采用物探对溶洞形态和尺寸进行初步测量,测得该含水层宽约2.5 m,深度13~16 m,与开挖方向同向斜交,与水平方向的夹角约为 80°。根据钻探地质报告,渗流压力约为 5.5 MPa,渗透系数约为 2×10-4 m/s。根据以上参数得到预测涌水量与实测涌水量的对比。结果表明(图14),涌水量随时间变化计算值与实测值具有相同规律,其中计算瞬时涌水量为 92 t/d,大于实测值 83 t/d。这是因为实测数据通常具有延迟性。涌水量随时间持续增大至 60 d后,由于溶洞采用灌浆和密封,导致涌水量下降。在 130 d后,涌水量明显下降到 20 t/d。此外,根据 130 d内的实测值和计算值对比发现,由于计算值无法考虑灌浆处理对涌水量的影响,因此,计算值与实测值相对误差会增大。

图13太子山隧道涌水突泥灾害
a—隧道涌水;b—隧道突泥
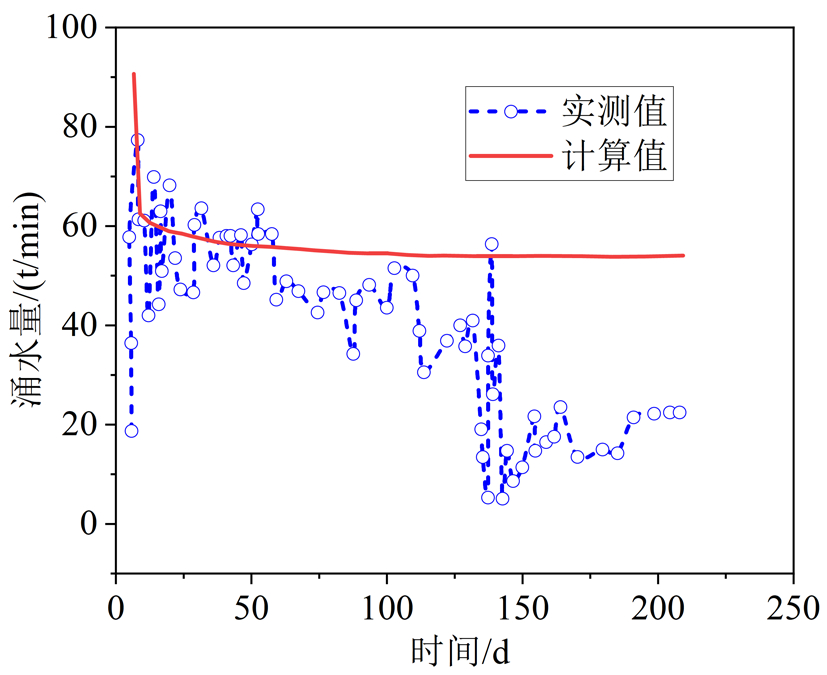
图14太子山隧道涌水量验证
3.2 新七道梁隧道
新七道梁隧道位于兰州市七里河,为典型的双洞单向行车隧道。隧道长度超过 4000 m,半径为 5.2 m,最大埋深超过500 m。其中,进口段隧洞穿越 F4 断层。受岩性和结构面控制,构造裂隙发育,富水带集中。其中,上盘岩体为中厚状灰岩夹千枚岩,下盘为砂岩夹泥岩。在 2002 年 7—8 月隧道开挖期间出现多处涌水和渗水工问题,属于典型的断层型涌水。调查统计,仅在XK 21+045~XK 20+825 里程段拱顶及左右边墙出现大小不一的涌水和渗水问题。根据现场调查及物探表明,隧道涌水控制性 F4 断裂带厚度约 15 m,与水平方向的倾角约为 76°,断裂带的渗透系数为1.2×10-4 m/s。
图15为新七道梁隧道涌水量实测数据与本文理论计算对比结果。可见理论计算值与实测值具有较高的吻合度。随时间增大,隧道涌水量逐渐趋于稳定。根据实测结果,当涌水时间增大至 10 d 后,隧道涌水量趋于稳定。实测稳定涌水量约为30 t/d,预测稳定涌水量约为 33 t/d,两者相对误差为 10 %,证明本文理论模型是可行的。
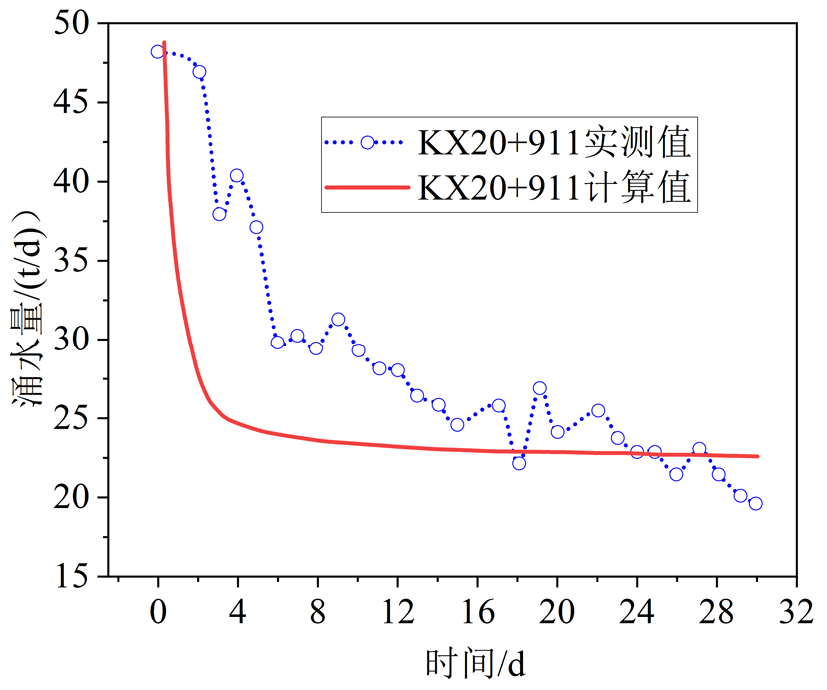
图15新七道梁隧道涌水量验证
4 结论
本文利用经典水文学原理,提出了一种预测隧道涌水量的半解析方法,并与现场实测数据对比检验了模型推导的正确性。具体得到如下3点结论:
(1)隧道涌水量与含水层渗透系数成正比,随涌水时间增大,初始涌水量显著降低,随后隧道涌水量逐渐趋于稳态。此外,含水层越厚,储水量越大,涌水量达到稳定所需的时间也越长。
(2)保持含水层渗透系数、宽度和隧道半径等参数不变,隧道涌水量与初始水位成正比,与其他参数相比,贮水率对隧道涌水量的影响不显著。
(3)采用本文模型对太子山隧道和新七道梁隧道涌水量预测结果与现场实测数据吻合度较高,证明本文模型可行。














