摘要
廊道区地质环境差异大,道路管道沿线灾害数量多、危害大,严重威胁人民生命财产安全。地质灾害易发性评价能够预测孕灾环境下灾害空间分布,但评价单元范围大小的划分不合理必然使得主次因子交叉与贡献率混杂现象,导致结果不可信。鉴于此,本文以谋道—建南道路管线线性廊道区与道路管线沿线 1000 m缓冲区为研究对象,探索廊道区地质灾害易发评价适宜单元范围大小、评价因子体系及适宜评价模型。研究表明,10 m×10 m评价单元最适宜作为沿线缓冲区地质灾害易发性评价单元,5 m×5 m评价效果最不明显;沿线缓冲区相对整体线性廊道区更适用做廊道地质灾害易发性评价区,基于粗糙集理论的模糊综合评价模型评价准确度高于贡献率-信息量耦合模型,为评价模型中最优评价模型。研究结果可为廊道区地质灾害防治研究提供参考。
Abstract
There are great differences in geological environment in the corridor area, and there are many disasters along the road and pipeline, which seriously threaten the safety of people's lives and property. The geological hazard susceptibility assessment can predict the spatial distribution of disasters under the disaster pregnant environment, but the unreasonable division of the assessment unit range inevitably leads to the phenomenon of primary and secondary factors crossing and contribution rate mixing, which leads to unreliable results. In view of this, taking the linear corridor area of the Moudao-Jiannan road pipeline and the 1000 m buffer zone along the road pipeline as the research object, the suitable unit range, evaluation factor system and suitable evaluation model for geological disaster prone evaluation in the corridor area are explored. Research shows: 10 m×10 m assessment unit is suitable for the geological hazard susceptibility assessment unit in the buffer zone along the line, and the 5 m×5 m evaluation effect is the least obvious; compared with the overall linear corridor area, the buffer area along the line is more suitable as the corridor geological disaster susceptibility evaluation area, the fuzzy comprehensive evaluation model based on rough set theory has higher evaluation accuracy than the contribution rate information coupling model, which is the best evaluation model in the evaluation model. The results can provide reference for the study of geological disaster prevention in corridor area.
0 引言
廊道区具有地质条件多样,自然条件复杂,线路长等特点,地质灾害频发(黄发明等,2021;王瑞瑞和刘冰,2022),且灾害多围绕道路与管道沿线,严重威胁廊道及居民的生命财产安全。因此,针对廊道区的地质灾害易发性评价为当下研究的重点与热点。其研究成果可为廊道区防灾减灾及保护生命财产安全提供有效帮助。
地质灾害易发性评价,其合理性与准确度受评价范围影响,其实质是不同单元范围大小的特征因子构成及其敏感性差异较大,评价单元大小的划分不合理必然存在主次因子交叉与贡献率混杂现象。因此,针对廊道区探索地质灾害易发评价适宜单元范围大小、评价因子体系及适宜评价模型极有必要。
于宪煜(2016)通过多尺度进行易发性评价分析了研究范围重要性,杨晨晨等(2020)利用地质背景资料和遥感影像确定9种易发性评价因子。从前人研究中看出,评价因子研究主要围绕单一评价区,而不同评价区因子体系是否相同研究甚少。由于地质背景不同,岩土体类型及物理力学性质的差异,导致其孕灾模式不同,不同的评价区应有独立的因子体系,忽略研究区地质环境选择的因子体系会直接影响易发性评价准确性。国内外学者为提高易发性评价准确度对评价模型做了深入研究(江思义等,2021;解明礼等,2021;李信等,2022),以信息量模型(杨淞月等,2021)、粗糙集模型(程温鸣等,2013),模糊数学综合评价模型(崔志超等, 2020)、人工神经网络模型(唐睿旋等,2017;Munzo et al.,2020)、频率比模型(Jesudasan et al.,2021)、支持向量机模型(Indrajit et al.,2021)、逻辑回归模型 (Goyes and Hernandez,2020;Sun et al.,2021)、聚类分析模型(黄发明等,2018)为主。其中,杨淞月等 (2021)利用信息量模型对鹤峰县城区滑坡灾害进行风险评价,为当地政府地灾防治提供理论依据。程温鸣等(2013)将粗糙集理论引入滑坡易发性建模中,分析出致灾因子敏感性,从而得出秭归县滑坡灾害易发性图。信息量模型与模糊数学模型由于目的明确,操作简单,适应性强的特点,被广泛用于地质灾害易发性评价,但信息量模型会受数据库不均衡的影响而大大降低精确性,模糊数学又会因主观性太强而降低结果说服力,而多模型耦合的方法克服了单一模型因子客观权重主观性的缺点并吸纳了两者优点(唐川和马国超,2015;马啸等, 2022;焦伟之等,2022)。
综上所述,本文以线性廊道区(大范围)与道路与管线 1000 m 缓冲区(小范围)为研究区,以 30 m× 30 m、10 m×10 m、5 m×5 m 栅格单元为评价单元。进而构建廊道区因子体系与缓冲区因子体系,利用信息量模型、贡献率-信息量模型与基于粗糙集理论的模糊数学综合评价模型对比验证准确度。探索廊道区易发性评价的适宜评价单元范围、因子组合及评价模型。
1 廊道区易发性评价流程
1.1 范围、因子及模型确定
线性廊道地质分区为基础,首先,根据地质环境背景和线性工程作用范围确定线性廊道评价区与线性工程沿线缓冲评价区。然后,根据地质背景与廊道区地质环境背景大致相同特点,确定线性廊道区评价因子与线性廊道区主控因子以及线性工程作用缓冲区重点因子组成的线性廊道缓冲区评价因子集。最后,对比贡献率-信息量模糊与粗糙模糊评价模型评价结果,以提高模型准确度,选择廊道区适宜评价模型。
1.2 核心步骤
①地质灾害评价范围与因子优化分析。首先,确定谋道-建南线性廊道区评价因子集,计算因子敏感性,利用贡献率-信息量模型分析 30 m×30 m、 10 m×10 m与5 m×5 m栅格单元分辨率下的易发性,并通过ROC验证得优势评价单元。其次,结合所得优势评价单元,沿线1000 m缓冲评价区分别使用线性廊道区评价因子集和沿线缓冲评价区因子进行敏感性分析,利用贡献率-信息量耦合模型计算易发性,ROC验证得适宜评价范围及评价因子。②地质灾害评价模型分析。基于评价范围研究,结合粗糙集理论,分析相关因素对应敏感性,进而构建模糊数学综合评价模型,通过成功率曲线验证,分析廊道区基于粗糙集理论的模糊数学综合评价模型、贡献率-信息量模型准确度。
2 易发性模型分析
2.1 贡献率模型
贡献率是一种利用数学统计定量分析各因子敏感系数的方法,由数量贡献率F(ρi)、面积贡献率C(ρi)及体积贡献率K(ρi)共3类指标的综合贡献率构建发育敏感性系数R(ρi),表示公式如下:
(1)
式(1)中,ρi(n)为影响因子第 i 区间的发育敏感性系数 Fe(ρi),Ce(ρi)及 Ke(ρi)分别为第 i 区间的发育频次贡献指数、发育面积贡献指数及发育体积贡献指数。
其次通过均值化处理,计算区间权重,各评价因子的敏感性采用因子间互权重系数进行特征表达。影响因子间的互权重计算公式如下:
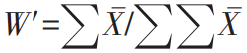
(2)
式(2)中,W'为影响因子的互权重,其中:。分别为影响因子高、中、低贡献区间或子类的贡献率平均值。
2.2 信息量模型
信息量模型是一种最广泛用于地质灾害易发性评价的模型之一。其特点是利用实测值定量计算得地质灾害孕育和发生概率的大小,易发程度表示清晰。
首先应用GIS空间分析技术分析地在灾害空间分布情况,确定评价因子分级内灾害分布,统计各评价因子间灾害点个数(Ni)与总个数(N)、灾害面积(Si)与总面积(S),将信息量表示如下:
(3)
式(3)中信息量值 Ii越大,表示其易发程度越高。
2.3 基于粗糙集理论的敏感性分析
基于粗糙集理论的模糊数学综合评价,以适宜评价范围为研究对象,为综合分析多因子累积作用,借程温鸣等(2013)对评价因子空间特征分析经验,对适宜评价范围易发性分析。首先挑选出部分有代表性的地灾点进行试验,这些点需具有全局代表性的特点。利用粗糙集理论中知识约简和属性重要性理论确定权重,以此通过对部分试验分析结果全面掌握总体效果,具有计算简便,操作简单等特点。
粗糙集理论是一种研究模糊性和不确定性的数学工具,在分类不变的基础上,利用知识约简法导出决策和规划。
2.3.1 知识约简
知识库中敏感性存在差异,在知识库不变情况下,对因子冗余处理,删除其中不敏感因子。其具体定义如下:
若 N 为一族等价关系,Nx∈N,若 ind(N)=ind(N-Nx),即称 Nx为 N 中不必要等价关系,否则 Nx为 N 中必要。设不同的等价关系(评价因子)N1,···,Nx∈N,论域 U关于 ind(N)的等价类以及删除某一因子后的等价类如下:
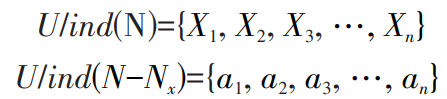
(4)
若 U/ind(N)=U/ind(N-Nx),即 Nx视为冗余因素,对其进行约简。
2.3.2 确定敏感性系数
粗糙集理论通过计算因子重要程度来确定因子敏感性。
由上式(4)等价关系知,N的信息量定义为:
(5)
式(5)中,[card(U)]表示集合 X 所含元素个数。属性重要性问题通过属性集 N 中去掉某一因素 Np 后的信息量变化来反映重要程度,将其表示为:
(6)
设 N={N1,N2,N3,···,Nm},则 Ni的权重 ai(i=1,2,3,···,m)可定义为:
(7)
ai的大小可以反映因子敏感性,ai值越大,表明因子敏感性越高,反之越低。
2.3.3 易发性评价模型构建
基于粗糙集理论的模糊数学综合评价模型,即克服了模糊数学模型的主观性较强,又弥补了传统分类法单指标或小指标分类。本文通过粗糙集理论得出的影响因素与对象间模糊运算得模糊评价结果。
首先,确定被评价对象评价指标。为综合分析多因子累积作用,基于粗糙集理论敏感性分析,选取发育度最高且具有良好代表性与相似性的两因子做约束因子,剩余评价因子代入公式(2)计算其敏感性。归一化处理后,将两个约束因子叠加至该图层组成被评价对象因素集,即模糊权向量。表示为D=(d1,d2,d3,d4,···)。
其次,确定被评价对象评价集。即对易发性程度分级,且每个等级都有对应一个模糊子集。按易发程度分为低、中、高、极高易发四个子集,并选取模糊分布原理下的K次抛物线分布函计算隶属度。
隶属函数如下:
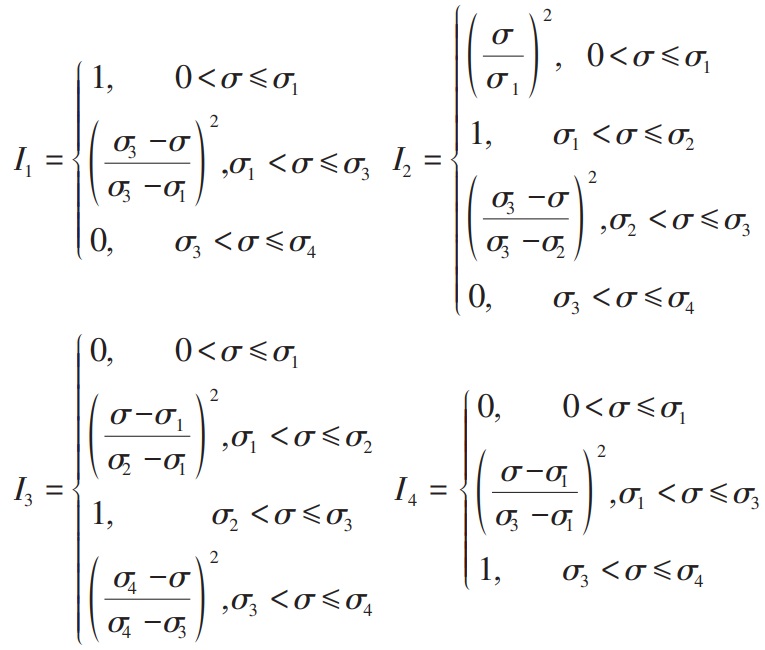
(8)
式(8)中,I1,I2,I3,I4分别代表被评价对象的低、中、高、极高易发等级隶属度;σ 为被评价对象实测值;σ1,σ2,σ3,σ4分别代表评价对象的界限值。
利用上述所得隶属度构造判断矩阵R:
(9)
由权向量D与判断矩阵R计算模糊综合评价结果P。模糊综合评价表示为:
(10)
式(10)中,P 为评价等级 I 上模糊子集 cj( j=1,2,···,m),表示被评价对象隶于等级Ii的程度。
最终,利用最大隶属度原则,得到评价对象隶属等级:
(11)
3 工程实例分析
3.1 研究区概况
研究区位于利川市鄂西南边陲,地跨东经 108° 30'00″~108°48'45″,北纬 30°17'30″~30°27'30″。东西宽约 18 km、南北长约 28 km,总面积 336 km²( 图1)。地处鄂西南近东西向展布的褶皱山区,属于云贵高原东北部的延伸部分,以近东西走向的褶皱山地为主,属于构造溶蚀侵蚀中低山区地貌,由于特殊地形条件,形成了峡谷、丘陵、山间盆地及河谷平川相互交错的地貌特征。
区内线性工程密集,涉及线性工程主要有G318 国道、恩广高速(G5012)、宜万铁路、利川—建南输气管线和川气东输管线。地处鄂西山区,山高坡陡、地形切割严重。特殊的自然地理环境和地质构造背景与人类工程活动对小型灾害的影响,使廊道沿线地质灾害发育规律:点多规模小,以岩质、浅层灾害为主,多分布在重要线性工程两侧及人类聚居区附近,危险及危害性较大。调查发现区内地质环境问题主要表现为崩塌与滑坡。发育地质灾害点 50 处,其中滑坡 17 处、崩塌 33 处,其中小型灾害 41 处,岩质 50 处,浅层崩滑 50 处,分别占比 82%, 100%,100%,道路管线较为发育。

图1利川市谋道—建南线性廊道区交通位置图
3.2 数据来源
基于利川谋道-建南地质调查资料与GIS分析,本文易发性数据源主要有:①地灾点数据来源于湖北省线性廊道区斜坡灾害易发性评价研究——以利川市为例项目数据。②地形数据来源于中国科学院计算机网络信息中心公布的 30 m DEM 数据。 ③道路、水系数据来源于1∶10000实际材料图。
3.3 地质灾害评价范围分析
3.3.1 评价范围与评价单元确定
据上述分区与范围选取原则,结合线性廊道区现场调查及资料分析,选取谋道—建南线性廊道区 (大范围)与道路管线沿线 1000 m 缓冲区(小范围) 作为本次评价范围(图2),选取 30 m×30 m、10 m× 10 m和5 m×5 m的栅格单元为评价单元。
图2研究区范围
a—利川谋道—建南线性廊道评价区;b—道路管线沿线1000 m缓冲评价区
3.3.2 评价因子与评价范围分析
首先,结合地质背景及资料分析,确定线性廊道区评价因子集(因子组合1)由地层岩性、坡度、坡向、曲率、湿度、道路构成。并由式(2)计算因子分因子敏感性,利用贡献率-信息量耦合模型计算 30 m×30 m、10 m×10 m、5 m×5 m分辨率下易发性,如表1所示。最后,为方便不同分辨率下易发性对比,进行易发性制图(图3)。对比得结果如下:分辨率越高其易发性分区越分散,但 3 种分辨率求得的易发性具有相似趋势,均表现出高易发区主要分布在西部道路、管线与水系密集区受人类工程活动影响程度较大,低易发区主要分布在东部地区,与现场调 (勘)察结果一致,且 3 种不同分辨率下易发性评价准确度较高。
表1大范围因子敏感性与信息量

图3贡献率-信息量模型易发性图
a—30 m×30 m;b—10 m×10 m;c—5 m×5 m
3.3.3 ROC曲线精度验证
ROC 曲线是一种广泛用于地质灾害评价的精度验证曲线。该曲线分别以信息量值由高到低区域面积累计百分比和样本点累计百分比做横轴和纵轴。曲线线下面积越大,表明预测结果准确度越高。AUC值与准确性对照如表2所示:
表2AUC值与准确性对照


图4成功率曲线
利用 ROC 曲线对谋道—建南评价区不同分辨率评价检验,结果如图4所示:AUC 值均介于 0.8~0.9,准确性较高。
由表1及 ROC 曲线结果显示:谋道—建南道路管线线性廊道区因子敏感性:地层>道路>坡度>曲率 >湿度 >坡向,且地层、道路、坡度因子占比 58.2%,与曲率、湿度、坡向因子权值差距较大;线性廊道区贡献率-信息量耦合模型评价易发结果:10 m×10 m分辨率下AUC值(0.822)>30 m×30 m分辨率下 AUC 值(0.815)>5 m×5 m 分辨率下 AUC 值 (0.788)。因此,评价结果与分辨率非线性相关,低分辨率与高分辨率对真实地貌信息及环境因子属性特征的弱化均使准确度低,而 10 m×10 m 分辨率下廊道区易发性评价所得结果准确度最高,为优势评价单元。
据上述因子选取原则,选取线性廊道区道路管线沿线缓冲区评价因子集(因子组合 2),廊道沿线评价区地形起伏较大且多分布在水系附近,特选高程、起伏度、水系作为廊道沿线评价因子,与谋道— 建南主控因子共同构成廊道沿线评价因子集。基于上述评价单元研究,在廊道沿线评价区以 10 m× 10 m栅格单元计算小范围因子敏感性与信息量(表3),易发性制图如图5所示。并对比 10 m×10 m 评价单元下线性廊道区与道路管线 1000 m 缓冲区不同因子组合下易发准确度(图6)。

图5沿线缓冲区因子10 m×10 m分辨率易发性图
综上得,1000 m 沿线缓冲区因子敏感性:地层岩性>道路>高程>坡度>起伏度>水系;栅格单元与评价因子相同条件下,廊道沿线区 AUC 值(0.829)>谋道—建南区AUC值(0.822);栅格单元与评价范围相同条件下,廊道沿线因子易发性 AUC 值(0.840)>谋道—建南因子易发性 AUC 值(0.829);因此,不同范围评价有独立因子体系,以谋道—建南区主控因子与廊道沿线区重点因子组成的评价因子体系相比原有因子体系更优,且谋道—建南评价区较大范围评价区更合理、适宜。
表3沿线缓冲区因子敏感性及信息量


图6成功率曲线
4 地质灾害评价模型分析
4.1 基于粗糙集理论的因素敏感性分析
基于上述评价范围分析,选取准确率更高的廊道沿线评价区研究。首先,利用GIS空间分析,选取具有代表性的 10 个采样点,统计 7 项试样指标(表4),结合上述相关标准与规范制定离散规则(表5),随后对统计的试验数据进行离散,所得结果如表7所示。
表4地灾点物理指标

注:评价因子分别用其首字母代替。DC—岩性,GC—高程,PD—坡度, QFD—泥石流强度,SX—斜坡稳定性,DL—地裂缝。
表5试样数据离散规则
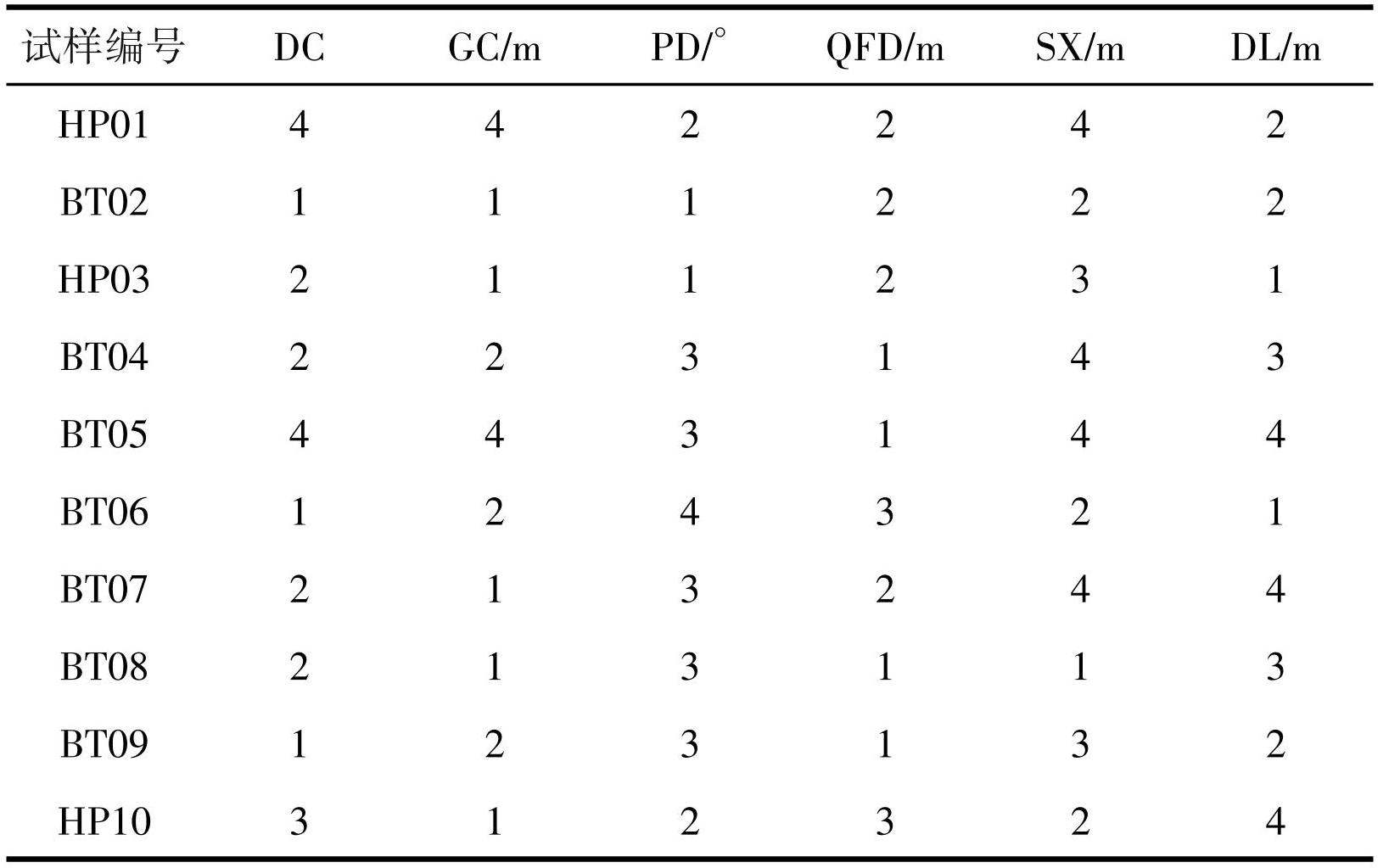
由上表4知,论域U = {1,2,3,4,5,6,7,8,9,10}评价指标R = {DC,GC,PD,PX,QFD,SX,DL},因此:
U/DC = { { 2, 6, 9}, {3, 4, 8}, {1, 5} { 7, 10}}
U/GC = {{ 2, 3, 7, 8, 10}, { 4, 6, 9}, {1, 5}}
U/PD = {{ 2, 3}, {1, 10}, { 4, 5, 6, 8, 9}, { 6}}
U/QFD = {{ 4, 5, 8, 9}, {1, 2, 3, 7}, { 6, 10}}
U/SX = {{1, 4, 5, 7}, { 2, 6, 10}, {3, 9}, {8}}
U/DL = {{1, 2, 9}, {3, 6}, { 4, 8}, { 5, 7, 10}}
对各因素简约处理,如下:
U/R={{1}, { 2}, {3}, { 4}, { 5}, { 6}, { 7}, {8}, { 9}, {10}}
U/ (R-DC) ={{1}, { 2, 3}, { 4, 8, 9}, { 5, 7}, { 6}, {10}}
U/ (R-GC) ={{1}, { 2}, {3}, { 4, 5, 8}, { 6}, { 7}, { 9}, {10}}
U/ (R-PD) ={{1, 5}, { 2}, {3}, { 4, 8}, { 6}, { 7}, { 9}, {10}}
U/ (R-QFD) ={{1, 5}, { 2}, {3}, { 4, 8}, { 6}, { 7, 10}, { 9}}
U/ (R-SX) = {{1}, { 2, 3}, { 4, 8, 9}, { 5}, { 6}, { 7, 10}}
U/ (R-DL) = {{1}, { 2, 3}, { 4, 5, 8, 9}, { 6}, { 7}, {10}}
由上可知,所选评价因子无冗余。由式(7)计算得,地层岩性、高程、坡度、起伏度、水系、道路隶属度分别为20%,12%,8%,12%,20%,28%,即因子重要程度:道路>地层岩性=水系>高程=起伏度=坡度,同时验证谋道-建南主控因子同样适用廊道区,选取两个评价区均高于平均因子权重的道路与地层岩性因子作为主控因子。选取主控因子作为约束因子,对高程、坡度、起伏度、水系进行敏感性叠加计算得各因子敏感性为 0.273,0.267,0.254, 0.206。进行归一化处理,将地层岩性和道路两约束因子叠加至该图层,组成模糊权向量 A=(126, 0.280,0.200,0.139,0.107,0.132)。
4.2 模糊数学综合评价模型易发性研究
隶属等级按易发等级分为低、中、高、极高易发 4 级。根据易发等级划分隶属函数定义域边界值,如表6。选取 80 m×120 m 的渔网单元对评价区划分,得3806个渔网单元,利用式(8)分别计算隶属函数,式(10)计算对应模糊评价结果。以最大隶属原则,划分易发等级,以本次试样为例,并进行易发制图(表7,图7)。
表6隶属函数边界值
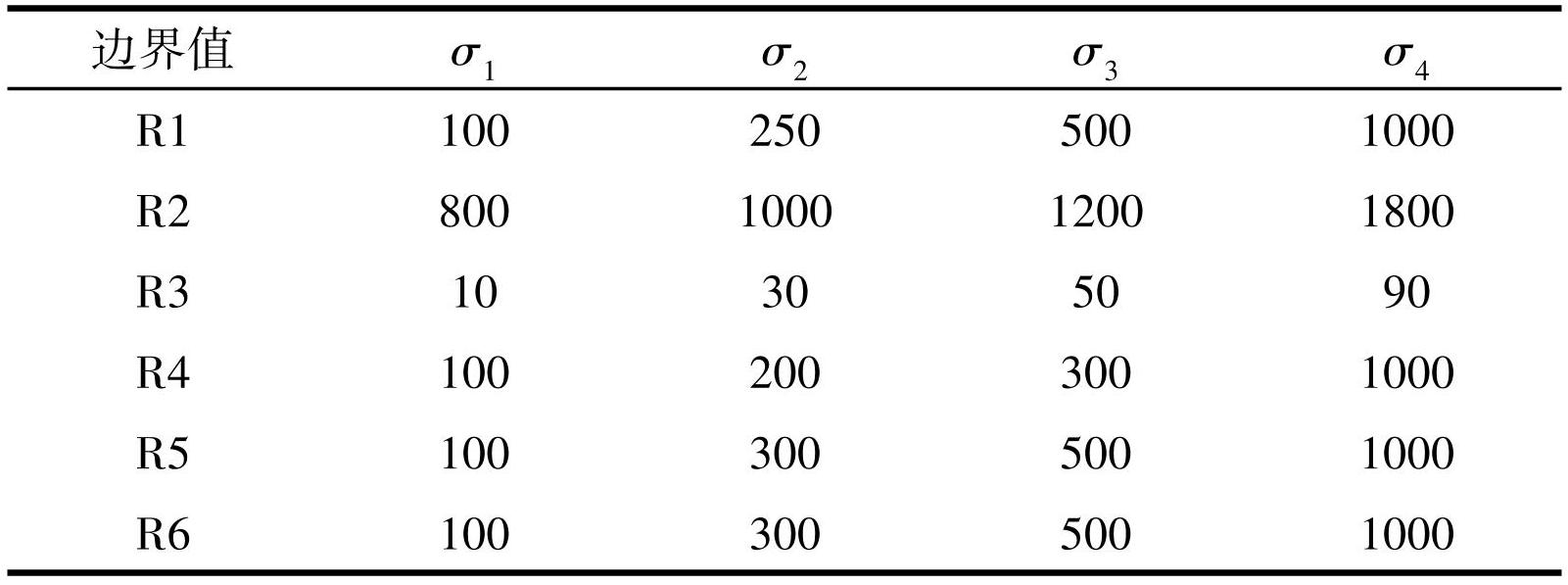
表7易发性评价结果
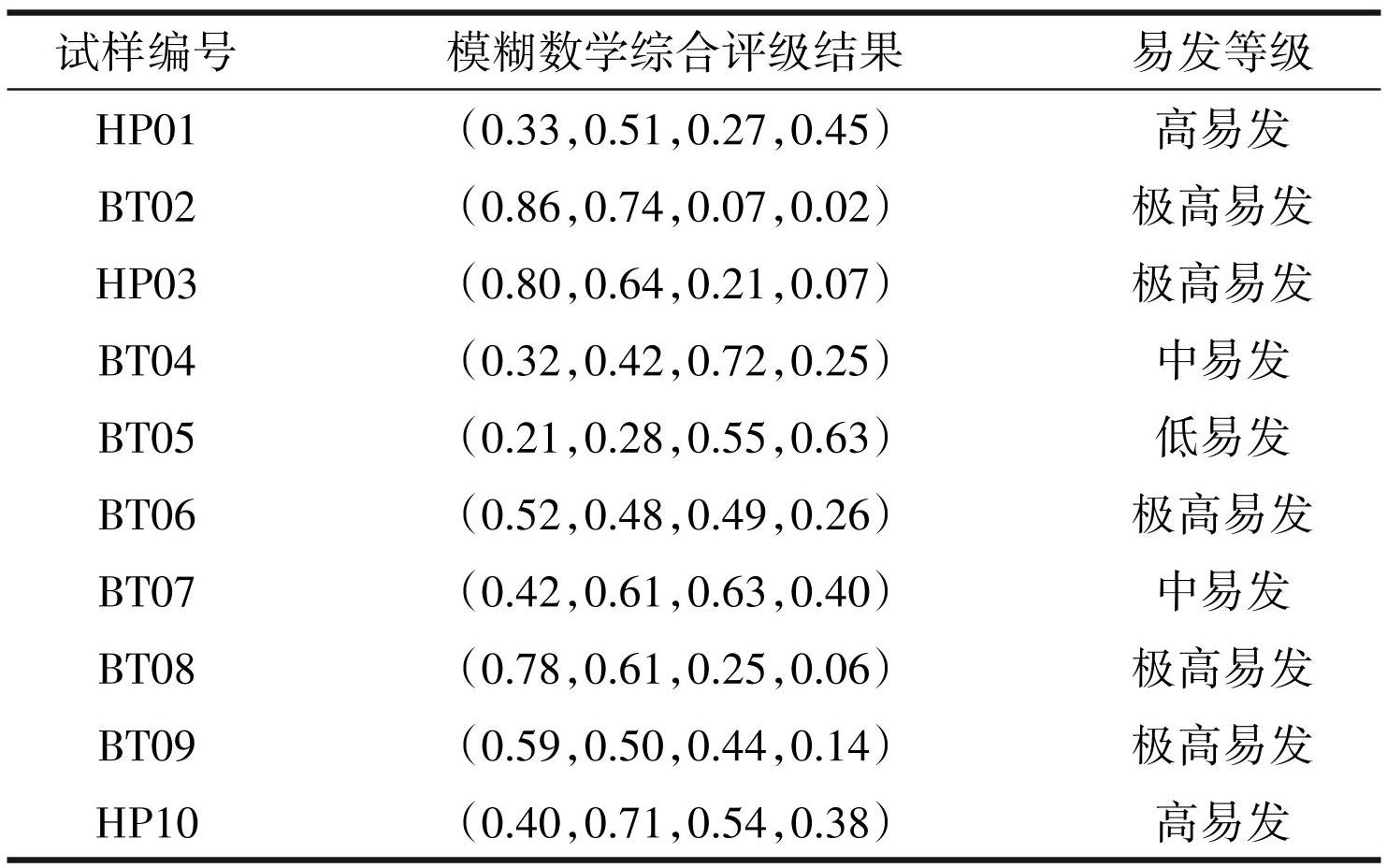

图7模糊数学模型易发性评价

图8成功率曲线
由图8ROC 精度验证结果显示,基于粗糙模糊数学评价模型的沿线缓冲评价区易发性 AUC 值 (0.851)>贡献率-信息量融合模型易发 AUC (0.840)。综上,本文 3种评价模型中粗糙模糊数学评价模型评价准确率高于贡献率与信息量耦合模型评价。因此,以上研究中基于粗糙集的模糊数学评价模型为评价最优模型。
5 结论
(1)评价单元范围大小与易发性准确度非线性相关,沿线缓冲区相对整体线性廊道区评价可信度高,适宜做廊道地质灾害易发性评价区,不同孕灾条件下因子组合不同,以沿线缓冲区主控因子与线性廊道区重点因子组成的评价因子体系相比原有单一因子体系更适宜沿线地质灾害易发性评价缓冲区。
(2)评价区与地质整体环境复杂程度相同条件下,不同栅格单元易发性评价结果存在差异。在廊道区评价范围中,10 m×10 m 栅格单元评价结果优于 30 m×30 m 栅格单元与 5 m×5 m 栅格单元评价结果。10 m×10 m栅格单元为优势评价单元,5 m×5 m 栅格单元评价效果最不明显。
(3)对比相同因子条件下两种评价范围的准确度,发现廊道沿线地质灾害易发性评价区为优势评价范围;并构建了以谋道—建南廊道区主控因子与廊道沿线区重点因子组成的评价因子体系,相比原有因子体系更优。
(4)廊道沿线地质灾害易发性评价区评价中,基于粗糙集理论的模糊数学易发性评价比贡献率-信息量易发性结果更准确,为本文易发评价模型中最优评价模型。所得结果可为廊道区地质灾害易发性评价研究提供参考。














